Question

Đã trả lời bởi chuyên gia

Answer 1

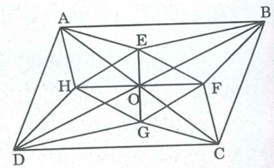
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Ta có: $∠$ (AOB) = $∠$ (COD) (đối đỉnh)

$∠$ (EOB ) = 1/2 $∠$ (AOB) (gt)

$∠$ (COG) = 1/2 $∠$ (COD) (gt)

Suy ra: $∠$ (EOB ) = $∠$ (COG)

$∠$ (EOB) + $∠$ (BOC) + $∠$ (COG) = 2 $∠$ (EOB) + $∠$ (BOC)

Mà $∠$ (AOB ) + $∠$ (BOC) = $180^{0}$ ( kề bù).Hay 2 $∠$ (EOB) + $∠$ (BOC ) = $180^{0}$

Suy ra: E,O,G thẳng hàng

Ta lại có: $∠$ (BOC) = $∠$ (AOD ) ( đối đỉnh)

$∠$ (HOD) = 1/2 $∠$ (AOD) (gt)

$∠$ (FOC) = 1/2 $∠$ (BOC) (gt)

Suy ra: $∠$ (HOD) = $∠$ (FOC)

$∠$ (HOD) + $∠$ (COD ) + $∠$ (FOC) = 2 $∠$ (HOD) + $∠$ (COD)

Mà $∠$ (AOD) + $∠$ (COD) = $180^{0}$ ( kề bù). Hay 2 $∠$ (HOD) + $∠$ (COD) = $180^{0}$

Suy ra: H, O, F thẳng hàng

$∠$ (ADO) = $∠$ (CBO) ( so le trong)

$∠$ (HDO) = $∠$ (FBO) ( chứng minh trên)

OD = OB ( t/chất hình bình hành)

$∠$ (HOD) = $∠$ (FOB ) ( đối đỉnh)

Do đó: $∆$ BFO = $∆$ DHO (g.c.g)

⇒ OF = OH

$∠$ (OAB) = $∠$ (OCD) ( so le trong)

$∠$ (OAE) = 1/2 $∠$ (OAB ) (gt)

$∠$ (OCG) = 1/2 $∠$ (OCD) (gt)

Suy ra: $∠$ (OAE) = $∠$ (OCG)

Xét $∆$ OAE và $∆$ OCG,ta có :

$∠$ (OAE) = $∠$ (OCG) ( chứng mình trên)

OA = OC ( t/chất hình bình hành)

$∠$ (EOA) = $∠$ (GOC) ( đối đỉnh)

Do đó: $∆$ OAE= $∆$ OCG (g.c.g) ⇒ OE = OG

Suy ra tứ giác EFGH là hình bình hành ( vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH

Vậy tứ giác EFGH là hình thoi

...Xem thêm

Answer 2