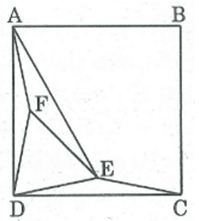
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho (EDC) = (ECD) =
Chứng minh rằng tam giác ABE là tam giác đều.
Quảng cáo
1 câu trả lời 683
Xét ADE và BCE , ta có:
ED = EC (vì AEDC cân tại E)
(ADE) = (BCE) =
AD = BC (gt)
Suy ra: ADE = BCE (c.g.c)
⇒ AE = BE (1)
* Trong ADE, ta có:
(AFD) = – ((FAD) + (FDA) ) = – ( + ) =
(AFD) + (DFE) + (AFE) =
⇒ (AFE) = - ((AFD) + (DFE) ) = – ( + ) =
* Xét AFD và AFE, ta có: AF cạnh chung
(AFD) = (AFE) =
DE = EF (vì DFE đều)
Suy ra: AFD = AFE (c.g.c) ⇒ AE = AD
Mà AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE
Vậy AEB đều.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!