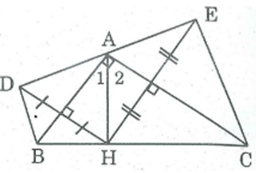
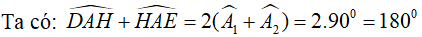Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC. Chứng minh rằng D đối xứng với E qua A.
Quảng cáo
1 câu trả lời 582
Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ADH cân tại A
Suy ra: AB là tia phân giác của (DAH)
⇒ (DAB) =
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ AHE cân tại A
Suy ra: AC là đường phân giác của góc (HAE) ⇒ = (EAC)
⇒ D, A, E thẳng hàng
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915