Question

Đã trả lời bởi chuyên gia

Answer 1

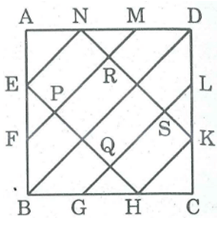
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Diện tích hình vuông ABCD bằng 6.6 = 36 ( $c m^{2}$ )

Diện tích $△$ BEH bằng 1/2 .4.4 = 8 ( $c m^{2}$ )

Diện tích $△$ DKN bằng 1/2 .4.4 = 8 ( $c m^{2}$ )

Diện tích phần còn lại là: 36 - (8 + 8) = 20 ( $c m^{2}$ )

Trong tam giác vuông AEN, ta có:

$E N^{2} = A N^{2} + A E^{2}$ = 4 + 4 = 8 ⇒ EN = 2 $\sqrt{2}$ (cm)

Trong tam giác vuông BHE, ta có:

$E H^{2} = B E^{2} + B H^{2}$ = 16 + 16 = 32 ⇒ EH = 4 $\sqrt{2}$ (cm)

Diện tích hình chữ nhật ENKH bằng: 2 $\sqrt{2}$ . 4 $\sqrt{2}$ = 16 ( $c m^{2}$ )

Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH được chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 $c m^{2}$

Diện tích $△$ AEN bằng 1/2 .2.2 = 2 ( $c m^{2}$ )

Vậy $S_{A E P S N} = S_{A E N} + S_{E P S N}$ = 2 + 16/4 = 6 ( $c m^{2}$ )

...Xem thêm

Answer 2