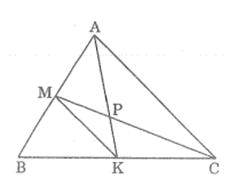
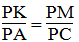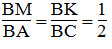Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết AP = 2PK và CP = 2PM. Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC
Quảng cáo
1 câu trả lời 448
Xét PAC và PKM,ta có:
Suy ra:
Lại có:(APC) = (KPM) (đối đỉnh)
Suy ra: PKM đồng dạng PAC(c.g.c) với tỉ số đồng dạng k = 1/2
Suy ra: 
Vì PKM đồng dạng PAC nên (PKM) = (PAC)
Suy ra: KM //AC (vì có cặp góc ở vị trí so le trong bằng nhau)
Trong ABC, ta có: KM // AC
Suy ra: BMK đồng dạng BAC (g.g)
Suy ra: 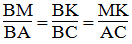
Từ 1 và (2) suy ra:
Vì BM = 1/2 BA nên M là trung điểm AB.
Vì BK = 1/2 BC nên K là trung điểm BC.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!