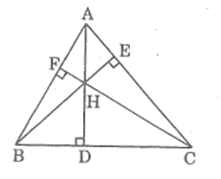
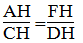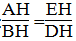Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH
Quảng cáo
1 câu trả lời 1554
Xét AFH và CDH, ta có:
(AFH) = (CDH) =
(AHF) = (CHD) (đối đỉnh)
Suy ra: AFH đồng dạng CDH (g.g)
Suy ra:
Suy ra: AH.DH = CH.FH (1)
Xét AEH và BDH,ta có:
(AEH) = (BDH) =
(AHE) = (BHD) (đối đỉnh)
Suy ra: AEH đồng dạng BDH (g.g)
Suy ra:
Suy ra: AH.DH = BH.EH (2)
Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!