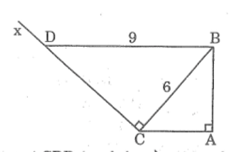
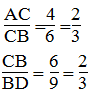Cho tam giác ABC vuông tại A, AC =4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD =9cm. Chứng minh rằng BD // AC
Quảng cáo
1 câu trả lời 1321
Xét hai tam giác vuông ABC và CDB, ta có:
(BAC) = (DCB) = (1)
Mà:
Suy ra: 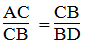
Từ (1) và (2) suy ra: ABC đồng dạng CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: (ACB) = (CBD)
⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )
nguyenthihueabcd1234@gmail.com
· 3 năm trước
Cho ∆ABC vuông tại A, có cạnh AB=12,BC=15. Từ C kẻ tia Cx vg góc với BC (tia Cx và điểm A nằm khác phía đối với đường thẳng BC). Từ B kẻ tia Bn sao cho
nguyenthihueabcd1234@gmail.com
· 3 năm trước
Góc BCn = ACB. Cx và Bn cắt nhau ở D
nguyenthihueabcd1234@gmail.com
· 3 năm trước
Tính diện tích của tam giác BCD
nguyenthihueabcd1234@gmail.com
· 3 năm trước
Giúp mình với
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915
Gửi báo cáo thành công!