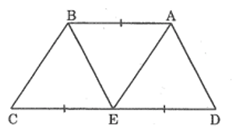
Hình thang ABCD (AB // CD) có CD= 2AB. Gọi E là trung điểm của CD. Chứng minh rằng ba tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một.
Quảng cáo
1 câu trả lời 1521
Vì CD = 2AB (gt) nên AB = 1/2 CD
Vì E là trung điểm của CD nên DE = EC = 1/2 CD
Suy ra: AB = DE = EC
Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau
Xét AEB và CBE, ta có:
(ABE) = ( BEC)(So le trong)
(AEB) = (EBC) (so le trong)
BE cạnh chung
⇒AEB =CBE (g.c.g) (1)
Hình thang ABCE có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau
Xét AEB và EAD, ta có:
(BAE) = (AED)(so le trong)
(AEB) = (EAD) (so le trong)
AE cạnh chung
⇒ AEB =EAD(g.c.g) (2)
Từ (1) và (2) suy ra: ΔAEB = ΔCBE = ΔEAD
Vậy ba tam giác AEB; CBE và EAD đôi một đồng dạng
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17163
Đã trả lời bởi chuyên gia
17163 -
 Đã trả lời bởi chuyên gia
16092
Đã trả lời bởi chuyên gia
16092 -
 Đã trả lời bởi chuyên gia
10026
Đã trả lời bởi chuyên gia
10026 -
 Đã trả lời bởi chuyên gia
8937
Đã trả lời bởi chuyên gia
8937 -
 Đã trả lời bởi chuyên gia
8864
Đã trả lời bởi chuyên gia
8864 -
 Đã trả lời bởi chuyên gia
7517
Đã trả lời bởi chuyên gia
7517 -
 Đã trả lời bởi chuyên gia
5915
Đã trả lời bởi chuyên gia
5915