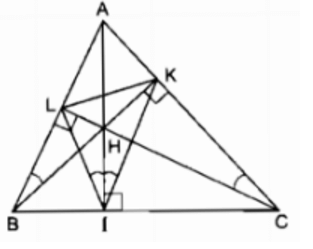
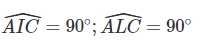Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ. Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
Quảng cáo
1 câu trả lời 412
Vì ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
Tứ giác AKHL có
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833