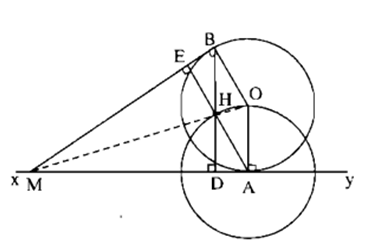
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
Quảng cáo
1 câu trả lời 500
Gọi BD, AE là đường cao của MAB. Ta có ΔMAE = MBD (cạnh huyền – góc nhọn) nên ME = MD, MHE = MHD (cạnh huyền – cạnh góc vuông) nên (EMH) = (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833
Gửi báo cáo thành công!