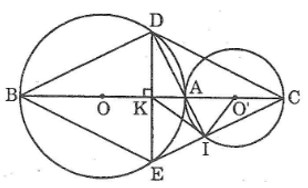
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài tại A (R > R’). Vẽ các đường kính AOB, AO’C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC. Chứng minh rằng tứ giác BDCE là hình thoi
Quảng cáo
1 câu trả lời 535
Vì đường tròn (O) và (O’) tiếp xúc ngoài tại A nên O, A và O’ thẳng hàng
Ta có: KB = KC (gt)
Trong đường tròn (O) ta có:
AB ⊥ DE tại K
Suy ra: KD = KE (đường kính vuông góc với dây cung)
Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Lại có: BC ⊥ DE
Suy ra tứ giác BDCE là hình thoi.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833
Gửi báo cáo thành công!