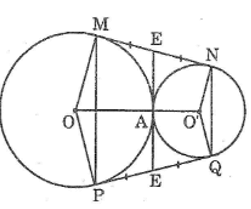
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng: MNQP là hình thang cân.
Quảng cáo
1 câu trả lời 501
Vì M và P đối xứng qua trục OO’ nên OO’ là đường trung trực của MP
Suy ra: OP = OM
Khi đó P thuộc (O) và MP ⊥ OO’ (1)
Vì N và Q đối xứng qua trục OO’ nên OO’ là đường trung trực của NQ
Suy ra: O’N = O’Q
Khi đó Q thuộc (O’) và NQ ⊥ OO’ (2)
Từ (1) và (2) suy ra: MP // NQ
Tứ giác MNQP là hình thang
Vì OO’ là đường trung trực của MP và NQ nên OO’ đi qua trung điểm hai đáy hình thang MNQP, OO’ đồng thời cũng là trục đối xứng của hình thang MNQP nên MNQP là hình thang cân.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833