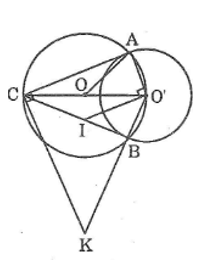
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O). Đường vuông góc với AO’ tại O’ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.
Quảng cáo
1 câu trả lời 444
Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: (tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => (hai góc so le trong)
Suy ra:
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: (tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => (hai góc so le trong)
Suy ra:
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833