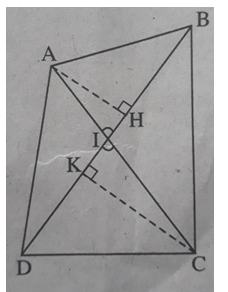
Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng = 1/2.AC.BD.sin.
Quảng cáo
1 câu trả lời 385
Giả sử hai đường chéo AC, BD cắt nhau tại I, (AIB) = là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin, CK = CI.sin
Diện tích tam giác ABD là = 1/2 BD.AH.
Diện tích tam giác CBD là = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin = 1/2BD.AC.sin
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833
Gửi báo cáo thành công!