tìm m để hàm số
có 2 điểm cực trị x1 x2 đều lớn hơn 0
Quảng cáo
2 câu trả lời 10160
Đáp án: $0<m<2$
Giải thích:
$y=\dfrac{1}{3}{{x}^{3}}-m{{x}^{2}}+\left( m+2 \right)x$
$y'={{x}^{2}}-2mx+m+2$
$\Delta {{'}_{y'}}={{m}^{2}}-\left( m+2 \right)$
$\Delta {{'}_{y'}}={{m}^{2}}-m-2$
Để $y$ có hai cực trị thì $y'$ phải có hai nghiệm phân biệt
$\Leftrightarrow\Delta{'}_{y'}>0$
$\Leftrightarrow m^2-m-2>0$
$\Leftrightarrow\left[\begin{array}{l}m>2\\m<-1\end{array}\right.$
Khi đó, theo hệ thức Vi-et, ta có: $\begin{cases}x_1+x_2=2m\\x_1x_2=m+2\end{cases}$
$y$ có hai cực trị lớn hơn $0$
$\Leftrightarrow\begin{cases}x_1+x_2>0\\x_1x_2>0\end{cases}$
$\Leftrightarrow\begin{cases}2m>0\\m+2>0\end{cases}$
$\Leftrightarrow\begin{cases}m>0\\m>-2\end{cases}$
$\Leftrightarrow m>0$
So với điều kiện, ta được kết quả cuối cùng là $0<m<2$
Vậy $0<m<2$ thì hàm số $y$ có hai điểm cực trị lớn hơn $0$
Quảng cáo
Bạn muốn hỏi bài tập?

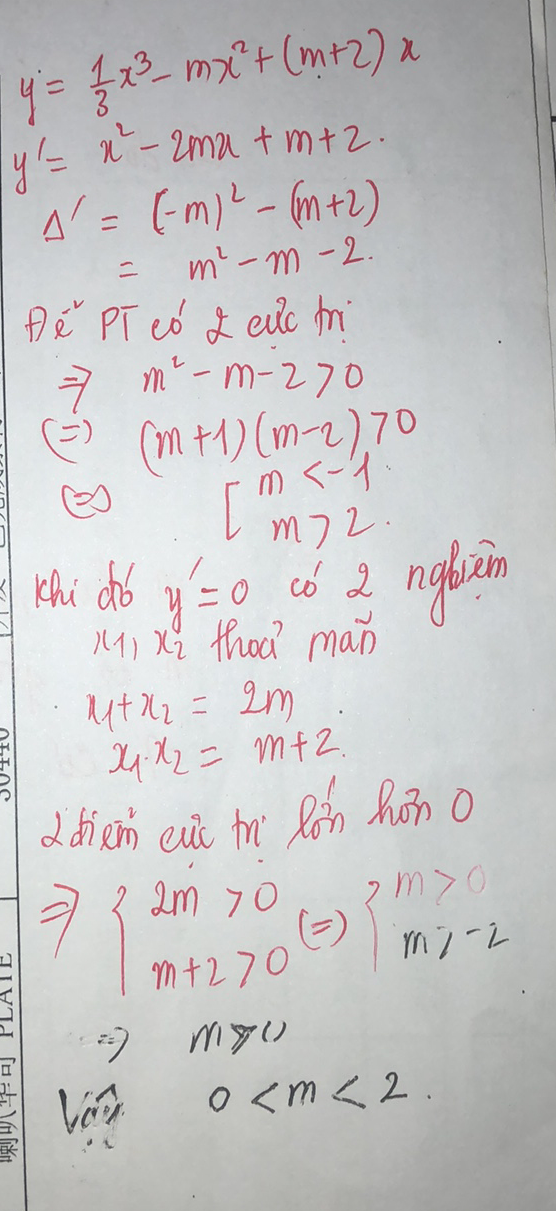 .
.
