Cho tam giác ABC cân tại A. Gọi H là trung điểm của BC.
a) Chứng minh: tam giác AHB = tam giác AHC
b) Từ H, kẻ Hx song song với AB, Hx cắt AC tại M.
Chứng minh: góc HAC= gócAHM và tam giác MHC cân tại M.
c) BM cắt AH tại O. Cho AB = 10cm, AH=6cm.Tính AO, HM.
d) Chứng minh: 2(AH + BM) > 3AB
Quảng cáo
1 câu trả lời 2683
a,
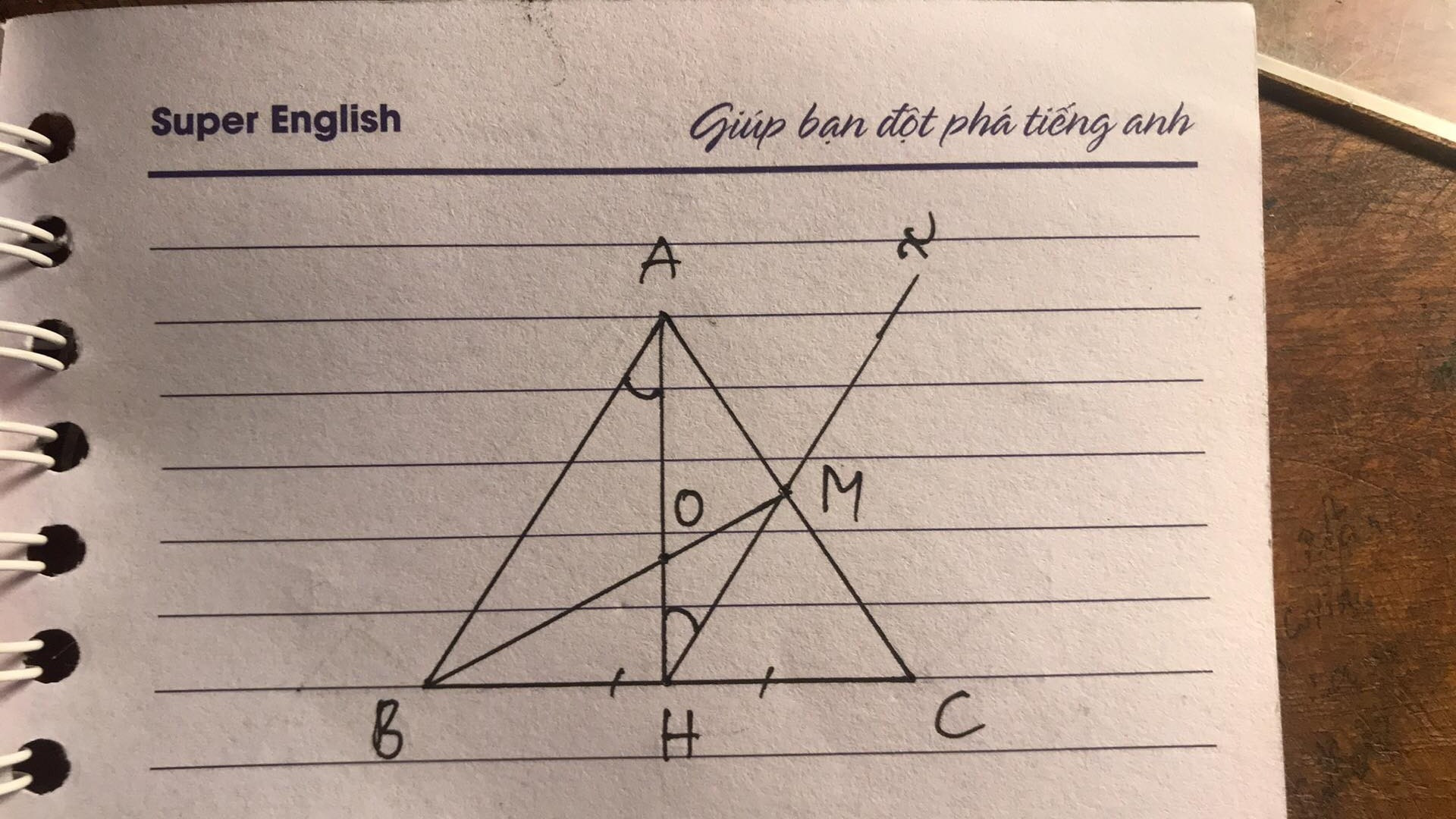
xét tam giác AHB và tam giác AHC có:
AB=AC ( do tam giác ABC cân tại A)
AH là cạnh chung
HB=HC (gt)
=> tam giác AHB=tam giác AHC (c.c.c)
b, do Hx // AB=> góc BAH=góc AHM (so le)
theo câu a=>góc BAH=góc CAH (góc tương ứng)
=> góc AHM=góc HAC (đpcm)
Lại có:
góc HAC+góc ACH=90 độ
góc AHM+gócMHC=90 độ
theo cmt ta có: góc AHM=góc HAC
=>góc ACH=góc MHC
xét tam giác MHC có:
góc MHC=góc MCH (cmt)
=> tam giác MHC cân tại M
c, xét tam giác ABC có: HB=HC; HM//AB
=> HM là đường trung bình của tam giác ABC
=> HM=1/2 AB=10/2=5 cm;
MA=MC=> BM là đường trung tuyến ứng với AC của tamm giác ABC
Xét tam giác ABC có 2 trung tuyến BM và AH cắt nhau tại O=> O là trọng tâm của tam giác ABC
=> AO=2/3 AH=6. 2/3=4 cm
d, Ta có: AG=2/3 AH; BG=2/3 BM
=> AG+BG=2/3.(AH+BM)
trong tam giác ABG có : GA+GB>AB
=> 2/3 (AH+BM)>AB
<=>2(AH+BM) >3 AB (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835


