a) Tính tổng các góc trong của đa giác 5 cạnh.
b) Cho ngũ giác đều ABCDE. Gọi F là giao điểm hai đường chéo AC và BE. Chứng minh tứ giác CFED là hình thoi.
Quảng cáo
1 câu trả lời 1169
5 năm trước
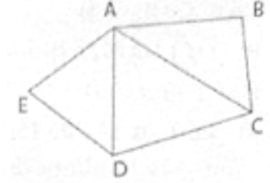
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 180o.
Tổng các góc trong của ngũ giác ABCDE là 180o.3 = 540o
b) Vì ABCDE là ngũ giác đều nên
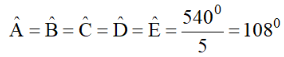
Mặt khác, ΔABC cân tại B nên:
![]()
Suy ra:
![]()
Lại có:
![]()
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt) nên tứ giác CEFD là hình thoi.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12666
Đã trả lời bởi chuyên gia
12666 -
 Đã trả lời bởi chuyên gia
11411
Đã trả lời bởi chuyên gia
11411 -
9654
-
 Đã trả lời bởi chuyên gia
5640
Đã trả lời bởi chuyên gia
5640 -
 Đã trả lời bởi chuyên gia
5324
Đã trả lời bởi chuyên gia
5324
Gửi báo cáo thành công!


