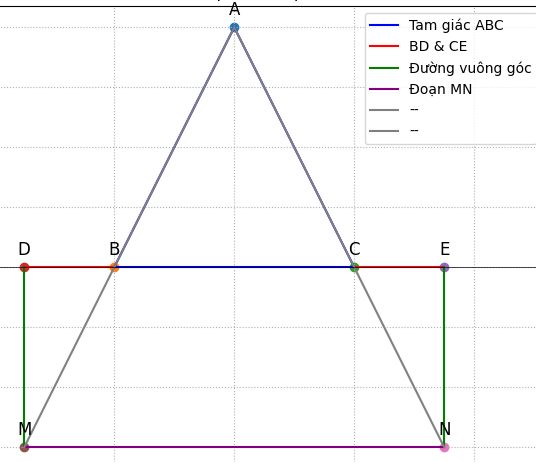
a: Chứng minh DM = EN
- Xét các góc:
Vì $∆$ABC cân tại A nên $\widehat{ABC}=\widehat{ACB}$.
$\widehat{MBD}=\widehat{ABC}$ (hai góc đối đỉnh).
$\widehat{NCE}=\widehat{ACB}$ (hai góc đối đỉnh).
=> $\widehat{MBD}=\widehat{NCE}$.
- Xét hai tam giác vuông $∆$MDB và $∆$NEC:
$\widehat{MDB}=\widehat{NEC}={90}^{\circ }$ (theo giả thiết MD $\perp$ BC và NE $\perp$ BC).
BD = CE (theo giả thiết).
$\widehat{MBD}=\widehat{NCE}$ (chứng minh trên).
=> $∆$MDB = $∆$NEC (Góc - Cạnh - Góc).
=> DM = EN (hai cạnh tương ứng).
b: Chứng minh IM = IN và BC < MN
- Chứng minh IM = IN:
- Xét hai tam giác vuông $∆$MDI và $∆$NEI:
$\widehat{MDI}=\widehat{NEI}={90}^{\circ }$.
DM = EN (chứng minh ở phần a).
$\widehat{DMI}=\widehat{ENI}$ (hai góc so le trong vì MD // NE do cùng vuông góc với BC).
=> $∆$MDI = $∆$NEI (Góc - Cạnh - Góc).
=> IM = IN (hai cạnh tương ứng).
- Chứng minh BC < MN:
+ Trong tam giác vuông MDI, cạnh huyền MI luôn lớn hơn cạnh góc vuông DI (MI > DI).
+ Tương tự, trong tam giác vuông NEI, cạnh huyền NI > EI.
=> MI + NI > DI + EI => MN > DE.
Mà DE = DB + BC + CE. Vì DB, CE > 0 nên DE > BC.
=> MN > BC.
c: Chứng minh $∆$BMO = $∆$CNO và điểm O cố định
- Xác định vị trí điểm O:
+ O nằm trên đường phân giác của góc A. Vì $∆$ABC cân tại A nên đường phân giác cũng là đường trung trực của BC. Suy ra OB = OC.
+ O nằm trên đường trung trực của MN (vì OI $\perp$ MN tại trung điểm I). Suy ra OM = ON.
- Chứng minh $∆$BMO = $∆$CNO:
- Xét $∆$BMO và $∆$CNO có:
BM = CN (do $∆$MDB = $∆$NEC => MB = NC).
OM = ON (chứng minh trên).
OB = OC (chứng minh trên).
=> $∆$BMO = $∆$CNO (Cạnh - Cạnh - Cạnh).
- Điểm O cố định
+ Điểm O là giao điểm của đường trung trực cạnh BC và đường phân giác góc A. Trong một tam giác ABC cố định, hai đường này trùng nhau hoặc cắt nhau tại các điểm xác định.
+ Thực tế, O là giao điểm của phân giác $\widehat{A}$ và trung trực của BC, vốn không phụ thuộc vào vị trí của D và E. Do đó, khi D, E thay đổi nhưng vẫn thỏa mãn điều kiện bài toán, O vẫn duy trì vị trí của nó.