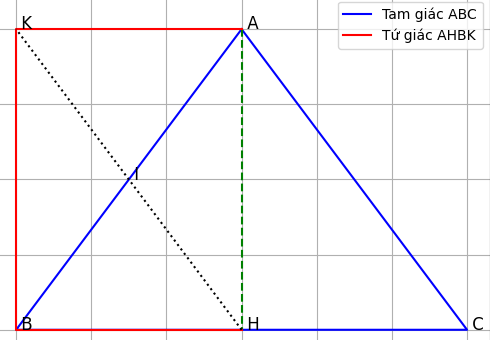
a) Tứ giác AHBK là hình gì? Vì sao?
- Xét tứ giác AHBK, ta có:
I là trung điểm của đường chéo AB (theo giả thiết).
I là trung điểm của đường chéo HK (do K đối xứng với H qua I).
=> Tứ giác AHBK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Lại có: AH là đường cao của tam giác ABC nên AH $\perp$ BC tại H.
=> AHB = 90$°$.
- Hình bình hành AHBK có một góc vuông ($\widehat{AHB}$ = 90$°$) nên là hình chữ nhật.
=> Tứ giác AHBK là hình chữ nhật.
b) Điều kiện để tứ giác AHBK là hình vuông
- Để hình chữ nhật AHBK trở thành hình vuông, ta cần thêm điều kiện hai cạnh kề bằng nhau:
AH = HB
- Xét tam giác ABC cân tại A:
+ Đường cao AH đồng thời là đường trung tuyến, suy ra H là trung điểm của BC.
=>  HB = $\frac{1}{2}$BC.
- Khi đó, điều kiện AH = HB tương đương với: AH =$\frac{1}{2}$BC
- Trong một tam giác, đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông.
- Do AH là trung tuyến ứng với cạnh BC và AH = $\frac{1}{2}$BC nên $∆$ABC vuông tại A.
- Kết hợp với giả thiết $∆$ABC cân tại A, ta có: Để tứ giác AHBK là hình vuông thì tam giác ABC phải là tam giác vuông cân tại A.

Bài toán:

Tam giác ABCABCABC cân tại AAA
AHAHAH là đường cao từ AAA xuống BCBCBC
III là trung điểm của ABABAB
KKK là điểm đối xứng của HHH qua III
Yêu cầu:
a) Xác định tứ giác AHBKAHBKAHBK
b) Điều kiện để tứ giác AHBKAHBKAHBK là hình vuông

a) Tứ giác AHBKAHBKAHBK là hình gì?
Bước 1: Xác định quan hệ các đoạn thẳng

Vì KKK đối xứng HHH qua III, nên:
I laˋ trung điểm của HK  ⟹  HI=IKI \text{ là trung điểm của } HK \implies HI = IKI laˋ trung điểm của HK⟹HI=IKIII cũng là trung điểm của ABABAB.
Bước 2: Xét tứ giác AHBKAHBKAHBK

Ta có:

HHH và KKK đối xứng nhau qua III
III là trung điểm của ABABAB → AB∥HKAB \parallel HKAB∥HK và AB=HKAB = HKAB=HK
Ngoài ra, AHAHAH và BKBKBK là các đường chéo cắt nhau tại trung điểm III.
Kết luận:

Tứ giaˊc AHBK laˋ hıˋnh bıˋnh haˋnh\text{Tứ giác } AH B K \text{ là hình bình hành} Tứ giaˊc AHBK laˋ hıˋnh bıˋnh haˋnhLý do: Hai đường chéo cắt nhau tại trung điểm → tứ giác là hình bình hành.

b) Điều kiện để tứ giác AHBKAHBKAHBK là hình vuông
Để hình bình hành trở thành hình vuông, cần:
hıˋnh bıˋnh haˋnh vừa coˊ caˊc cạnh ba˘ˋng nhau, vừa coˊ goˊc vuoˆng.\text{hình bình hành vừa có các cạnh bằng nhau, vừa có góc vuông.}hıˋnh bıˋnh haˋnh vừa coˊ caˊc cạnh ba˘ˋng nhau, vừa coˊ goˊc vuoˆng.Vì AHBKAHBKAHBK đã là hình bình hành → để là hình vuông:
Hıˋnh bıˋnh haˋnh phải laˋ hıˋnh chữ nhật vaˋ coˊ caˊc cạnh ba˘ˋng nhau  ⟹  △ABC phải caˆn vaˋ vuoˆng tại A.\text{Hình bình hành phải là hình chữ nhật và có các cạnh bằng nhau} \implies \triangle ABC \text{ phải cân và vuông tại A.}Hıˋnh bıˋnh haˋnh phải laˋ hıˋnh chữ nhật vaˋ coˊ caˊc cạnh ba˘ˋng nhau⟹△ABC phải caˆn vaˋ vuoˆng tại A.Kết luận:

Tam giác ABCABCABC cần cân tại AAA và vuông tại AAA thì tứ giác AHBKAHBKAHBK sẽ là hình vuông.


 
 
 

Bài toán:

Tam giác ABCABCABC cân tại AAA
AHAHAH là đường cao từ AAA xuống BCBCBC
III là trung điểm của ABABAB
KKK là điểm đối xứng của HHH qua III
Yêu cầu:
a) Xác định tứ giác AHBKAHBKAHBK
b) Điều kiện để tứ giác AHBKAHBKAHBK là hình vuông

a) Tứ giác AHBKAHBKAHBK là hình gì?
Bước 1: Xác định quan hệ các đoạn thẳng

Vì KKK đối xứng HHH qua III, nên:
I laˋ trung điểm của HK  ⟹  HI=IKI \text{ là trung điểm của } HK \implies HI = IKI laˋ trung điểm của HK⟹HI=IKIII cũng là trung điểm của ABABAB.
Bước 2: Xét tứ giác AHBKAHBKAHBK

Ta có:

HHH và KKK đối xứng nhau qua III
III là trung điểm của ABABAB → AB∥HKAB \parallel HKAB∥HK và AB=HKAB = HKAB=HK
Ngoài ra, AHAHAH và BKBKBK là các đường chéo cắt nhau tại trung điểm III.
Kết luận:

Tứ giaˊc AHBK laˋ hıˋnh bıˋnh haˋnh\text{Tứ giác } AH B K \text{ là hình bình hành} Tứ giaˊc AHBK laˋ hıˋnh bıˋnh haˋnhLý do: Hai đường chéo cắt nhau tại trung điểm → tứ giác là hình bình hành.

b) Điều kiện để tứ giác AHBKAHBKAHBK là hình vuông
Để hình bình hành trở thành hình vuông, cần:
hıˋnh bıˋnh haˋnh vừa coˊ caˊc cạnh ba˘ˋng nhau, vừa coˊ goˊc vuoˆng.\text{hình bình hành vừa có các cạnh bằng nhau, vừa có góc vuông.}hıˋnh bıˋnh haˋnh vừa coˊ caˊc cạnh ba˘ˋng nhau, vừa coˊ goˊc vuoˆng.Vì AHBKAHBKAHBK đã là hình bình hành → để là hình vuông:
Hıˋnh bıˋnh haˋnh phải laˋ hıˋnh chữ nhật vaˋ coˊ caˊc cạnh ba˘ˋng nhau  ⟹  △ABC phải caˆn vaˋ vuoˆng tại A.\text{Hình bình hành phải là hình chữ nhật và có các cạnh bằng nhau} \implies \triangle ABC \text{ phải cân và vuông tại A.}Hıˋnh bıˋnh haˋnh phải laˋ hıˋnh chữ nhật vaˋ coˊ caˊc cạnh ba˘ˋng nhau⟹△ABC phải caˆn vaˋ vuoˆng tại A.Kết luận:

Tam giác ABCABCABC cần cân tại AAA và vuông tại AAA thì tứ giác AHBKAHBKAHBK sẽ là hình vuông.