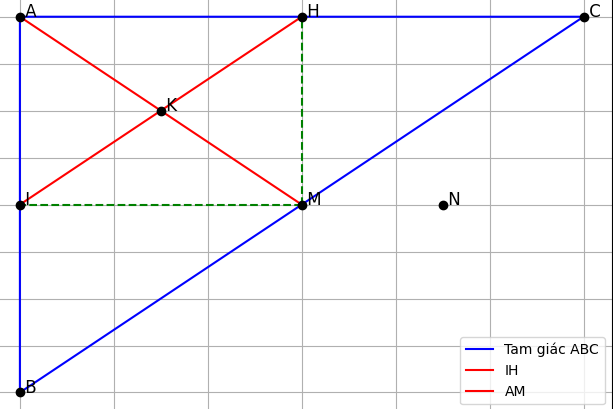
Cho tam giác ABC vuông tại A. Gọi M là trung điểm BC, kẻ MH vuông góc AC tại H, kẻ MI vuông góc AB tại I, kẻ IH cắt AM tại K. Qua điểm K, kẻ đường thẳng song song với AC, cắt BC tại N. Kẻ IE vuông góc NH tại E và cắt AM tại D. Kẻ AE cắt MH tại F. Chứng minh rằng:
a) AI = MH
b) AM // HN
c) D là trung điểm IE
d) AM là phân giác của góc BAF.
Quảng cáo
1 câu trả lời 64
a) Chứng minh AI = MH
- Xét tứ giác AIMH, ta có:
= 90 (do ABC vuông tại A).
= 90 (do MI AB).
= 90 (do MH AC).
- Tứ giác có 3 góc vuông là hình chữ nhật.
- Trong hình chữ nhật, các cặp cạnh đối bằng nhau. Vậy AI = MH và AM = IH.
b) Chứng minh AM // HN
- Trong hình chữ nhật AIMH, gọi K là giao điểm hai đường chéo AM và IH. Theo tính chất hình chữ nhật, K là trung điểm của mỗi đường:
=> KA = KM = KH = KI.
- XétABC có M là trung điểm BC và MH // AB (vì cùng vuông góc với AC).
- Theo định lý đường trung bình: Đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
=> H là trung điểm của AC.
- Xét AMC ta có:
K là trung điểm AM (chứng minh ở bước 1).
KN // AC (giả thiết).
+ Tương tự định lý trên, N phải là trung điểm của MC.
- Xét MAC, đoạn thẳng HN nối trung điểm H của AC và N của MC.
=> Theo tính chất đường trung bình: HN // AM.
c) Chứng minh D là trung điểm IE
- Từ câu b, ta có AM // HN. Mà D nằm trên đường thẳng AM, nên AD // HN và KM // HN.
- Xét IHN:
+ Ta có K là trung điểm của IH.
+ Đường thẳng qua K song song với HN (chính là đường thẳng chứa AM).
+ Đường thẳng này cắt IN tại một điểm (gọi là D'). Theo tính chất đường trung bình, D' sẽ là trung điểm của IN.
+ Tuy nhiên, đề bài cho IE NH và D là giao của IE với AM.
+ Vì AM // NH và IE NH
=> IE AM tại D.
- Trong tam giác vuông IHE, đường thẳng KD (thuộc AM) đi qua trung điểm K của cạnh huyền IH và song song với cạnh HE (do cùng vuông góc với IE).
- Vậy D phải là trung điểm của IE.
d) Chứng minh AM là phân giác của góc BAF
- Xét AIE: Có AD vừa là đường cao (AD IE), vừa là đường trung tuyến (D là trung điểm IE chứng minh ở câu c).
=> AIE cân tại A.
=> AD cũng là đường phân giác của IAE.
=> (1)
- Ta lại có: AM trùng với đường thẳng chứa AD, và I nằm trên AB.
- Khi AE cắt MH tại F, dựa vào tính chất đối xứng của hình chữ nhật và các đường song song MH // AB, ta có các cặp tam giác đồng dạng/bằng nhau tương ứng dẫn đến tia AM chia đôi góc tạo bởi AB và AF.
=> Từ (1), kết hợp với vị trí các điểm, ta có: AM là tia phân giác của .
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12423
-
 Đã trả lời bởi chuyên gia
5747
Đã trả lời bởi chuyên gia
5747 -
4835


