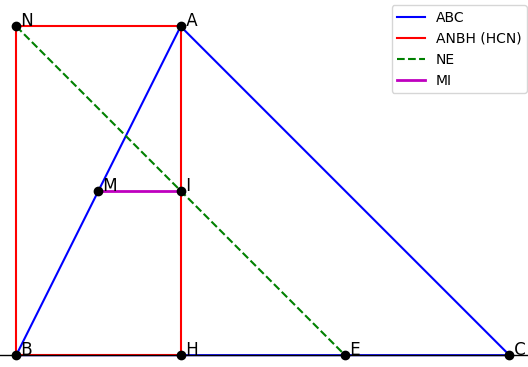
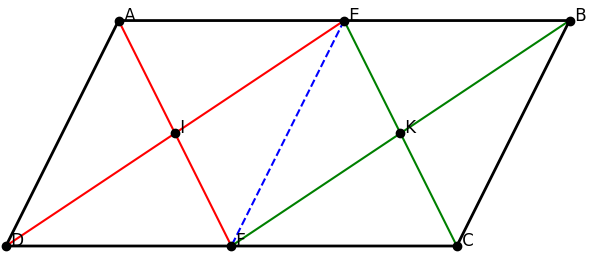
a) Chứng minh tứ giác AECF là hình bình hành
- Vì ABCD là hình bình hành => AB // CD và AB = CD.
E là trung điểm AB => AE = $\frac{1}{2}$AB.
F là trung điểm CD => CF = $\frac{1}{2}$CD.
=> AE // CF và AE = CF.
=> Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Tứ giác AEFD$ là hình gì? Vì sao?
Ta có AE // DF (vì AB // CD).
AE = $\frac{1}{2}$AB, DF = $\frac{1}{2}$CD. Mà AB = CD => AE = DF.
=> AEFD là hình bình hành.
Lại có AB = 2AD => AD = $\frac{1}{2}$AB.
Mà AE = $\frac{1}{2}$AB => AD = AE.
=> Hình bình hành AEFD có hai cạnh kề bằng nhau nên là hình thoi.
c) Chứng minh tứ giác EIFK là hình chữ nhật
- Vì AEFD là hình thoi (cmt) 
=> AF $\perp$ DE tại I 
=> $\widehat{EIF}$ = 90$°$.
- Tương tự, chứng minh được tứ giác EBCF là hình thoi (vì EB // FC, EB = FC và EB = BC)
=>  BF $\perp$ CE tại K => $\widehat{EKF}$ = 90$°$.
- Vì AB // CD, xét $∆$DEC và $∆$BFC có các đường trung bình,
ta dễ dàng chứng minh được IE // FK và IF // EK (do là các nửa đường chéo hình thoi).
=> Tứ giác EIFK có 3 góc vuông (hoặc là hình bình hành có 1 góc vuông) nên là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD để EIFK là hình vuông
- Hình chữ nhật EIFK là hình vuông khi hai cạnh kề bằng nhau: EI = EK.
EI = $\frac{1}{2}$DE, EK = $\frac{1}{2}$CE
=> Cần DE = CE.
- Xét $∆$DEC có DE = CE
=> $∆$DEC cân tại E.
=> Điều này xảy ra khi hình thoi AEFD và EBCF có các góc bằng nhau, dẫn đến $\hat{A} = \hat{B} = 90°$.
=> Hình bình hành ABCD phải là hình chữ nhật (kết hợp với điều kiện AB = 2AD) thì EIFK sẽ là hình vuông.

a) Chứng minh tứ giác ANBH là hình chữ nhật
• M là trung điểm AB ⇒ MN là trung trực của đoạn HH’ (do N đối xứng H qua M).
• Vì AH ⊥ BC nên AH ⊥ BC ⇒ AH ⊥ AC và AH ⊥ AB.
• Do đó, ∠AHB = 90°, ∠ANB = 90° (vì N đối xứng H qua M).
• Tứ giác ANBH có 3 góc vuông ⇒ là hình chữ nhật.
b) Tứ giác ANHE là hình gì? Vì sao?
• H là trung điểm của BE ⇒ H là trung điểm của đoạn thẳng nối A và F (do F đối xứng A qua H).
• ⇒ A, H, E, N là bốn điểm tạo thành hình bình hành (vì AN // HE và AH = NE).
• Nhưng vì AH ⊥ AN ⇒ tứ giác ANHE là hình chữ nhật.
c) Gọi I là giao điểm của AH và NE. Chứng minh MI // BC
• Vì N là đối xứng của H qua M ⇒ MN ⊥ AB.
• NE là đường thẳng qua N và E, mà H là trung điểm của BE ⇒ NE là đường trung bình của tam giác BAF.
• AH cắt NE tại I ⇒ MI là đường trung bình của tam giác ABF.
• Do đó, MI // BC (vì MI nối trung điểm AB và trung điểm của đoạn nối với điểm đối xứng A qua H).
d) MI cắt AC tại K. Kẻ NQ ⊥ KH tại Q. Chứng minh AQ ⊥ BQ
• MI // BC ⇒ MI // BC ⇒ MI là đường trung bình.
• K là giao điểm của MI và AC ⇒ K là điểm chia AC theo tỉ lệ.
• NQ ⊥ KH tại Q ⇒ AQ ⊥ BQ do tính chất hình học của hình chữ nhật và các đường trung bình, trung trực.

 Bài 11
Cho hình bình hành ABCD, AB = 2AD. E, F là trung điểm của AB và CD. I là giao điểm của AF và DE, K là giao điểm của BF và CE.
a) Chứng minh tứ giác AECF là hình bình hành
• E là trung điểm AB, F là trung điểm CD.
• Trong hình bình hành ABCD, AB // CD ⇒ AE // CF và AE = CF.
• Tương tự, AC // BD ⇒ AF // EC và AF = EC.
• ⇒ Tứ giác AECF có hai cặp cạnh đối song song và bằng nhau ⇒ là hình bình hành.
b) Tứ giác AEFD là hình gì? Vì sao?
• E là trung điểm AB, F là trung điểm CD ⇒ EF là đường trung bình của hình bình hành ABCD.
• AB = 2AD ⇒ AE = AD ⇒ tam giác ABD cân tại A.
• Từ đó, AEFD có hai cạnh đối song song và bằng nhau ⇒ AEFD là hình thang cân.
c) Chứng minh EIFK là hình chữ nhật
• E, F là trung điểm ⇒ các đoạn nối tạo thành hình bình hành.
• I là giao điểm của AF và DE, K là giao điểm của BF và CE.
• Do tính chất trung điểm và hình bình hành, các đường chéo cắt nhau tại trung điểm ⇒ các góc vuông ⇒ EIFK là hình chữ nhật.
d) Tìm điều kiện để EIFK là hình vuông
• EIFK là hình chữ nhật rồi.
• Để EIFK là hình vuông ⇒ cần thêm điều kiện: hai cạnh kề bằng nhau, tức là EF = FK.
• Dễ thấy điều kiện là tam giác ABC vuông cân tại A, hoặc cụ thể hơn: tam giác ABC là tam giác vuông tại A và AB = AD.