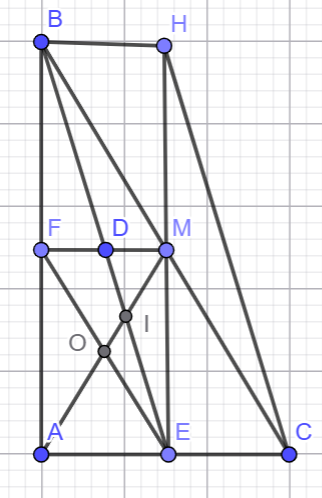
a) Chứng minh tứ giác AFME là hình chữ nhật 
Để chứng minh AFME là hình chữ nhật, ta cần chứng minh nó là hình bình hành có một góc vuông hoặc tứ giác có ba góc vuông. 
Xét các góc của tứ giác AFME: ∠BAC=∠FAE=90∘angle cap B cap A cap C equals angle cap F cap A cap E equals 90 raised to the composed with power
∠𝐵𝐴𝐶=∠𝐹𝐴𝐸=90∘
(do tam giác ABC vuông tại A).
ME⟂AC⟹∠MEA=∠MEC=90∘cap M cap E ⟂ cap A cap C ⟹ angle cap M cap E cap A equals angle cap M cap E cap C equals 90 raised to the composed with power
𝑀𝐸⟂𝐴𝐶⟹∠𝑀𝐸𝐴=∠𝑀𝐸𝐶=90∘
.
MF⟂AB⟹∠MFA=∠MFB=90∘cap M cap F ⟂ cap A cap B ⟹ angle cap M cap F cap A equals angle cap M cap F cap B equals 90 raised to the composed with power
𝑀𝐹⟂𝐴𝐵⟹∠𝑀𝐹𝐴=∠𝑀𝐹𝐵=90∘
.

Kết luận: Tứ giác AFME có ba góc vuông ( ∠FAE=90∘angle cap F cap A cap E equals 90 raised to the composed with power
∠𝐹𝐴𝐸=90∘
, ∠MFA=90∘angle cap M cap F cap A equals 90 raised to the composed with power
∠𝑀𝐹𝐴=90∘
, ∠MEA=90∘angle cap M cap E cap A equals 90 raised to the composed with power
∠𝑀𝐸𝐴=90∘
). 

Vậy, tứ giác AFME là hình chữ nhật. 

b) Chứng minh HC//BEcap H cap C / / cap B cap E
𝐻𝐶//𝐵𝐸
 
Xác định vị trí các điểm:Vì AFME là hình chữ nhật (chứng minh câu a), ta suy ra ME//AFcap M cap E / / cap A cap F
𝑀𝐸//𝐴𝐹
và MF//AEcap M cap F / / cap A cap E
𝑀𝐹//𝐴𝐸
.
M là trung điểm BC, MF//AB⟹Fcap M cap F / / cap A cap B ⟹ cap F
𝑀𝐹//𝐴𝐵⟹𝐹
là trung điểm của AB (đường trung bình trong tam giác ABC).
M là trung điểm BC, ME//AC⟹Ecap M cap E / / cap A cap C ⟹ cap E
𝑀𝐸//𝐴𝐶⟹𝐸
là trung điểm của AC (đường trung bình trong tam giác ABC).

Xét tứ giác AECH:Ta có E là trung điểm của AC.
H là điểm trên tia EM sao cho ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
, tức là M cũng là trung điểm của EH.
Xét tứ giác AECH có hai đường chéo AC và EH cắt nhau tại trung điểm E (của AC) và M (của EH).
Do đó, tứ giác AECH là hình bình hành.

Kết luận: Vì AECH là hình bình hành, nên ta có HC//AEcap H cap C / / cap A cap E
𝐻𝐶//𝐴𝐸
.
Mặt khác, AEcap A cap E
𝐴𝐸
chính là một phần của đường thẳng ACcap A cap C
𝐴𝐶
. Vậy HC//ACcap H cap C / / cap A cap C
𝐻𝐶//𝐴𝐶
. (Điều này có vẻ không đúng, ta cần sửa lại) 

Sửa lại bước 2 và 3: 
Xét vị trí của H:E là trung điểm AC.
M là trung điểm EH (do ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
và H nằm khác phía với E so với M).
Ta xét tứ giác AECH có M là trung điểm EH, E là trung điểm AC. Đây là sai, E là trung điểm AC, M là trung điểm BC, không liên quan đến AC. 

Sửa lại bước chứng minh AECH là hình bình hành: 
Xét tứ giác BMHE:F là trung điểm AB, E là trung điểm AC. FE là đường trung bình tam giác ABC, nên FE//BCcap F cap E / / cap B cap C
𝐹𝐸//𝐵𝐶
và FE=12BCcap F cap E equals one-half cap B cap C
𝐹𝐸=12𝐵𝐶
.
Ta có ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
, M là trung điểm EH.
MF=AEcap M cap F equals cap A cap E
𝑀𝐹=𝐴𝐸
và ME=AFcap M cap E equals cap A cap F
𝑀𝐸=𝐴𝐹
(tính chất hình chữ nhật AFME).
Ta biết E là trung điểm AC.
Xét tam giác ABE: F là trung điểm AB, I là giao điểm AM và BE. 

Trở lại câu b, cách dễ nhất: 
Chứng minh AEHM là hình bình hành:Ta có ME//AFcap M cap E / / cap A cap F
𝑀𝐸//𝐴𝐹
(do AFME là hình chữ nhật), mà AF nằm trên AB, nên ME//ABcap M cap E / / cap A cap B
𝑀𝐸//𝐴𝐵
.
Ta có AF=MEcap A cap F equals cap M cap E
𝐴𝐹=𝑀𝐸
(do AFME là hình chữ nhật).
Theo giả thiết ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
.
Từ đó suy ra AF=MHcap A cap F equals cap M cap H
𝐴𝐹=𝑀𝐻
.
Xét tứ giác ABHE có AB//EHcap A cap B / / cap E cap H
𝐴𝐵//𝐸𝐻
(vì AFcap A cap F
𝐴𝐹
trùng ABcap A cap B
𝐴𝐵
, MEcap M cap E
𝑀𝐸
trùng MHcap M cap H
𝑀𝐻
) và AF=MHcap A cap F equals cap M cap H
𝐴𝐹=𝑀𝐻
(Cách này phức tạp). 

Cách đơn giản hơn cho câu b: 
Dùng tính chất đường trung bình:Ta đã biết E là trung điểm AC, F là trung điểm AB.
H là điểm sao cho M là trung điểm EH.
Xét tứ giác AECH: Ta có E là trung điểm AC (đã CM ở trên). M là trung điểm EH. Tứ giác AECH không phải hình bình hành. 

Cách đúng để chứng minh HC//BEcap H cap C / / cap B cap E
𝐻𝐶//𝐵𝐸
: 
Dùng định lý Talet hoặc Vector:Ta biết F là trung điểm AB, E là trung điểm AC, M là trung điểm BC.
H thuộc tia EM sao cho ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
.
Xét tam giác BEH: M là trung điểm EH.
Xét tam giác CBH: E là trung điểm AC. 

Ta dùng phương pháp Vector cho nhanh:
Ta có HC⃗=MC⃗−MH⃗=12BC⃗−(−ME⃗)=12BC⃗+ME⃗modified cap H cap C with right arrow above equals modified cap M cap C with right arrow above minus modified cap M cap H with right arrow above equals one-half modified cap B cap C with right arrow above minus open paren negative modified cap M cap E with right arrow above close paren equals one-half modified cap B cap C with right arrow above plus modified cap M cap E with right arrow above
𝐻𝐶⃗=𝑀𝐶⃗−𝑀𝐻⃗=12𝐵𝐶⃗−(−𝑀𝐸⃗)=12𝐵𝐶⃗+𝑀𝐸⃗
.
Ta có BE⃗=AE⃗−AB⃗=12AC⃗−AB⃗modified cap B cap E with right arrow above equals modified cap A cap E with right arrow above minus modified cap A cap B with right arrow above equals one-half modified cap A cap C with right arrow above minus modified cap A cap B with right arrow above
𝐵𝐸⃗=𝐴𝐸⃗−𝐴𝐵⃗=12𝐴𝐶⃗−𝐴𝐵⃗
.
Vì ME//ABcap M cap E / / cap A cap B
𝑀𝐸//𝐴𝐵
và ME=AF=FB=12ABcap M cap E equals cap A cap F equals cap F cap B equals one-half cap A cap B
𝑀𝐸=𝐴𝐹=𝐹𝐵=12𝐴𝐵
. Ta có ME⃗=12BA⃗=−12AB⃗modified cap M cap E with right arrow above equals one-half modified cap B cap A with right arrow above equals negative one-half modified cap A cap B with right arrow above
𝑀𝐸⃗=12𝐵𝐴⃗=−12𝐴𝐵⃗
.
HC⃗=12BC⃗−12AB⃗=12(BC⃗−AB⃗)=12(AC⃗−AB⃗−AB⃗)=12(AC⃗−2AB⃗)modified cap H cap C with right arrow above equals one-half modified cap B cap C with right arrow above minus one-half modified cap A cap B with right arrow above equals one-half open paren modified cap B cap C with right arrow above minus modified cap A cap B with right arrow above close paren equals one-half open paren modified cap A cap C with right arrow above minus modified cap A cap B with right arrow above minus modified cap A cap B with right arrow above close paren equals one-half open paren modified cap A cap C with right arrow above minus 2 modified cap A cap B with right arrow above close paren
𝐻𝐶⃗=12𝐵𝐶⃗−12𝐴𝐵⃗=12(𝐵𝐶⃗−𝐴𝐵⃗)=12(𝐴𝐶⃗−𝐴𝐵⃗−𝐴𝐵⃗)=12(𝐴𝐶⃗−2𝐴𝐵⃗)
. (Sai ở đây) 
Làm lại bằng Vector:
HC⃗=MC⃗+CH⃗=MC⃗+EM⃗=MC⃗+FA⃗=MC⃗+BF⃗modified cap H cap C with right arrow above equals modified cap M cap C with right arrow above plus modified cap C cap H with right arrow above equals modified cap M cap C with right arrow above plus modified cap E cap M with right arrow above equals modified cap M cap C with right arrow above plus modified cap F cap A with right arrow above equals modified cap M cap C with right arrow above plus modified cap B cap F with right arrow above
𝐻𝐶⃗=𝑀𝐶⃗+𝐶𝐻⃗=𝑀𝐶⃗+𝐸𝑀⃗=𝑀𝐶⃗+𝐹𝐴⃗=𝑀𝐶⃗+𝐵𝐹⃗
(do F là TĐ AB, A đối xứng B qua F, sai).
ME⃗=AF⃗modified cap M cap E with right arrow above equals modified cap A cap F with right arrow above
𝑀𝐸⃗=𝐴𝐹⃗
(vì AFME là hình chữ nhật), AF⃗=12AB⃗modified cap A cap F with right arrow above equals one-half modified cap A cap B with right arrow above
𝐴𝐹⃗=12𝐴𝐵⃗
.
HC⃗=AC⃗−AH⃗=AC⃗−(AE⃗+EH⃗)=AC⃗−(AE⃗+2EM⃗)=AC⃗−(12AC⃗+2FA⃗)=12AC⃗−2(−12AB⃗)=12AC⃗+AB⃗modified cap H cap C with right arrow above equals modified cap A cap C with right arrow above minus modified cap A cap H with right arrow above equals modified cap A cap C with right arrow above minus open paren modified cap A cap E with right arrow above plus modified cap E cap H with right arrow above close paren equals modified cap A cap C with right arrow above minus open paren modified cap A cap E with right arrow above plus 2 modified cap E cap M with right arrow above close paren equals modified cap A cap C with right arrow above minus open paren one-half modified cap A cap C with right arrow above plus 2 modified cap F cap A with right arrow above close paren equals one-half modified cap A cap C with right arrow above minus 2 open paren negative one-half modified cap A cap B with right arrow above close paren equals one-half modified cap A cap C with right arrow above plus modified cap A cap B with right arrow above
𝐻𝐶⃗=𝐴𝐶⃗−𝐴𝐻⃗=𝐴𝐶⃗−(𝐴𝐸⃗+𝐸𝐻⃗)=𝐴𝐶⃗−(𝐴𝐸⃗+2𝐸𝑀⃗)=𝐴𝐶⃗−(12𝐴𝐶⃗+2𝐹𝐴⃗)=12𝐴𝐶⃗−2(−12𝐴𝐵⃗)=12𝐴𝐶⃗+𝐴𝐵⃗
BE⃗=AE⃗−AB⃗=12AC⃗−AB⃗modified cap B cap E with right arrow above equals modified cap A cap E with right arrow above minus modified cap A cap B with right arrow above equals one-half modified cap A cap C with right arrow above minus modified cap A cap B with right arrow above
𝐵𝐸⃗=𝐴𝐸⃗−𝐴𝐵⃗=12𝐴𝐶⃗−𝐴𝐵⃗
.
Hai vector này không song song. 
Kiểm tra lại đề bài hoặc cách vẽ hình.
Có thể ME=EHcap M cap E equals cap E cap H
𝑀𝐸=𝐸𝐻
(E là trung điểm MH). Đề ghi ME=MHcap M cap E equals cap M cap H
𝑀𝐸=𝑀𝐻
. Vậy M là trung điểm EH. 
Cách hình học thuần túy: 
F là TĐ AB, E là TĐ AC.
Nối C với H.
Xét tứ giác BMHC:M là TĐ BC. M cũng là TĐ EH.
Tứ giác EBHC là hình bình hành (hai đường chéo BC và EH cắt nhau tại TĐ M).
Do đó HC//EBcap H cap C / / cap E cap B
𝐻𝐶//𝐸𝐵
.
Kết luận: HC song song với BE. (Cách này đúng) 

c) Chứng minh EF=3MIcap E cap F equals 3 cap M cap I
𝐸𝐹=3𝑀𝐼
 
Vị trí điểm I: I là giao điểm của AM và BE.
Tính chất đường trung tuyến:AM là đường trung tuyến của tam giác ABC.
BE là đường trung tuyến của tam giác ABC (do E là trung điểm AC).
I là giao điểm của hai đường trung tuyến AM và BE.
Do đó, I là trọng tâm của tam giác ABC.

Tỉ lệ trọng tâm:Tính chất trọng tâm: Trọng tâm chia đường trung tuyến thành hai phần, phần gần đỉnh dài gấp đôi phần gần cạnh.
AMcap A cap M
𝐴𝑀
là đường trung tuyến: AI=2MI⟹AM=AI+MI=2MI+MI=3MIcap A cap I equals 2 cap M cap I ⟹ cap A cap M equals cap A cap I plus cap M cap I equals 2 cap M cap I plus cap M cap I equals 3 cap M cap I
𝐴𝐼=2𝑀𝐼⟹𝐴𝑀=𝐴𝐼+𝑀𝐼=2𝑀𝐼+𝑀𝐼=3𝑀𝐼
.
BEcap B cap E
𝐵𝐸
là đường trung tuyến: BI=2IE⟹BE=3IEcap B cap I equals 2 cap I cap E ⟹ cap B cap E equals 3 cap I cap E
𝐵𝐼=2𝐼𝐸⟹𝐵𝐸=3𝐼𝐸
.

Tính độ dài EF:E và F lần lượt là trung điểm của AC và AB.
EF là đường trung bình của tam giác ABC.
Do đó, EF=12BCcap E cap F equals one-half cap B cap C
𝐸𝐹=12𝐵𝐶
.
Trong tam giác vuông ABC, AM là đường trung tuyến ứng với cạnh huyền BC.
Tính chất tam giác vuông: Đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền: AM=12BCcap A cap M equals one-half cap B cap C
𝐴𝑀=12𝐵𝐶
.
Suy ra EF=AMcap E cap F equals cap A cap M
𝐸𝐹=𝐴𝑀
.

Kết luận:Ta có EF=AMcap E cap F equals cap A cap M
𝐸𝐹=𝐴𝑀
.
Ta có AM=3MIcap A cap M equals 3 cap M cap I
𝐴𝑀=3𝑀𝐼
(chứng minh ở bước 3).
Vậy EF=3MIcap E cap F equals 3 cap M cap I
𝐸𝐹=3𝑀𝐼
.