Cho tam giác ABC có đường cao AH. Vẽ đường tròn tâm A, có bán kính AH. Chứng minh BC là tiếp tuyếng tại tiếp điểm H của đường tròn.
Cho tam giác abc vuông tại a vẽ đường tròn (B;BA). Chứng minh AC là tiếp tuyến của đường tròn.
Quảng cáo
2 câu trả lời 81
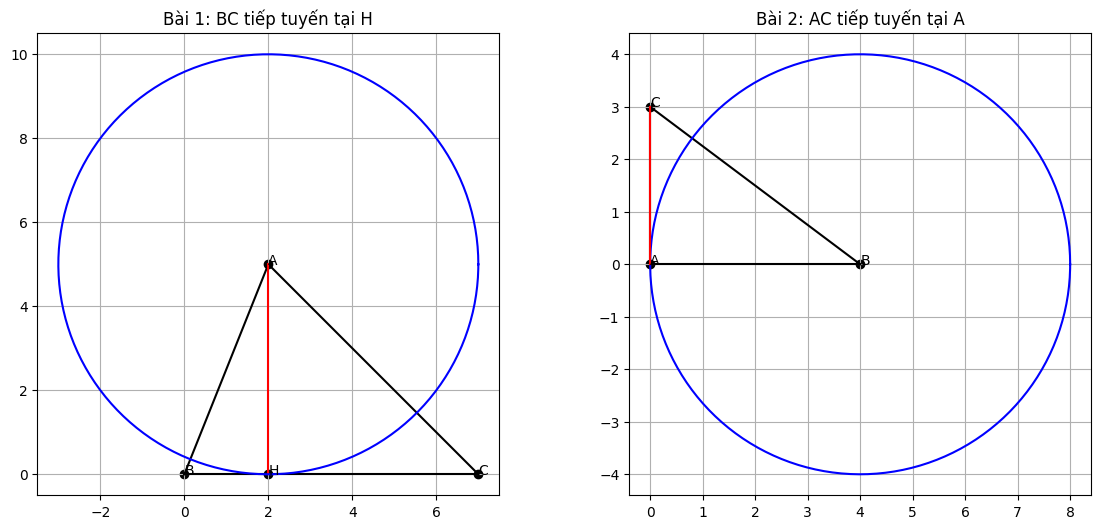
I. BÀI 1 – TIẾP TUYẾN TRONG TAM GIÁC ABC CÓ ĐƯỜNG CAO AH
Bài toán:
Cho tam giác ABC. AH là đường cao ⇒ AH ⟂ BC.
Vẽ đường tròn tâm A bán kính AH.
Chứng minh: BC là tiếp tuyến của đường tròn tại H.
=> Chứng minh
Ta có: tâm đường tròn là A, bán kính AH ⇒ H là điểm trên đường tròn.
Muốn chứng minh BC là tiếp tuyến tại H, ta chứng minh:
BC ⟂ AH (vì bán kính AH tại tiếp điểm phải vuông góc tiếp tuyến).
Nhưng theo giả thiết: AH ⊥ BC
Điều này đúng theo định nghĩa đường cao của tam giác.
Vậy: BC ⊥ AH = bán kính tại H ⇒ BC là tiếp tuyến của đường tròn.
=> BC là tiếp tuyến tại H.
II. BÀI 2 – TAM GIÁC ABC VUÔNG TẠI A
Bài toán:
Cho tam giác ABC vuông tại A.
Vẽ đường tròn tâm B, bán kính BA.
Chứng minh AC là tiếp tuyến của đường tròn tại A.
=> Chứng minh
Đường tròn có tâm B, bán kính BA ⇒ bán kính là BA, và A nằm trên đường tròn.
Để chứng minh AC tiếp tuyến tại A, ta cần: BA ⊥ AC
Nhưng tam giác ABC vuông tại A nên: AB ⊥ AC ⇒ bán kính BA vuông góc AC tại A
⇒ AC tiếp xúc với đường tròn tại A.
=> AC là tiếp tuyến tại A.
Phần 1: Chứng minh BC là tiếp tuyến của đường tròn tâm A, bán kính AH
Xác định mối quan hệ: Ta có AH là đường cao của tam giác ABC, do đó AH⟂BCcap A cap H ⟂ cap B cap C
𝐴𝐻⟂𝐵𝐶
tại H.
Xác định tiếp điểm: Đường tròn tâm A có bán kính là AH, và H là một điểm trên đường tròn. Do đó, H là tiếp điểm.
Kết luận: Vì BC vuông góc với bán kính AH tại tiếp điểm H, nên BC là tiếp tuyến của đường tròn tâm A.
Phần 2: Cho tam giác ABC vuông tại A, vẽ đường tròn (B;BA). Chứng minh AC là tiếp tuyến của đường tròn
Xác định tiếp điểm: Điểm A nằm trên đường tròn vì bán kính của đường tròn là BA và khoảng cách từ tâm B đến A là BA. Do đó, A là tiếp điểm.
Xác định mối quan hệ: Tam giác ABC vuông tại A, nên AC⟂ABcap A cap C ⟂ cap A cap B
𝐴𝐶⟂𝐴𝐵
tại A.
Kết luận: Vì AC vuông góc với bán kính AB tại tiếp điểm A, nên AC là tiếp tuyến của đường tròn (B;BA).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
8376
Đã trả lời bởi chuyên gia
8376 -
 Đã trả lời bởi chuyên gia
7885
Đã trả lời bởi chuyên gia
7885 -
 Đã trả lời bởi chuyên gia
6056
Đã trả lời bởi chuyên gia
6056 -
 Đã trả lời bởi chuyên gia
5833
Đã trả lời bởi chuyên gia
5833




