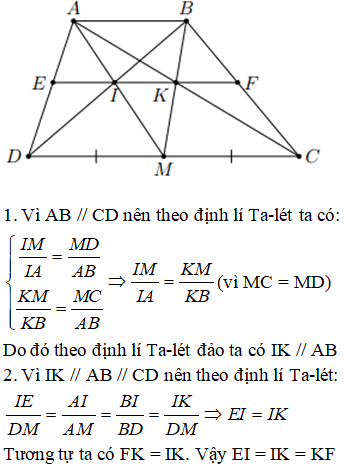
Cho hình thang ABCD (AB//CD) (AB=CD/2). M thuộc CD, kẻ đường qua M, // AC và đường qua M, // BD cắt AD và BC lần lượt tại F, E; EF cắt AC và BD tại H và K
a) Tình AO/AC và BO/BD (O là giao điểm AC và BD)
b) CMR: EH = HK = KF
Quảng cáo
3 câu trả lời 95
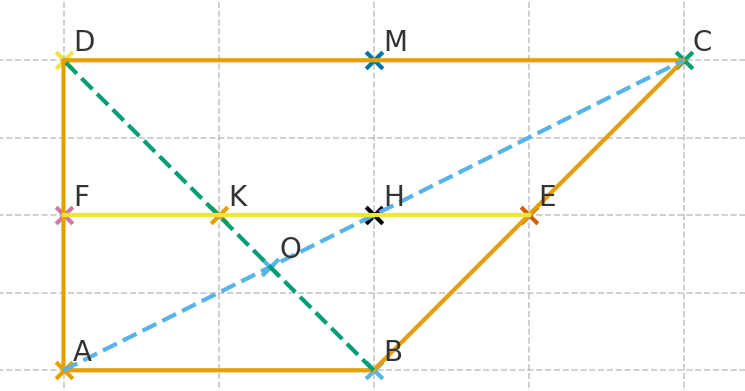
a) Tính AO/AC và BO/BD (O là giao điểm AC và BD)
Vì AB // CD nên ta có:
Xét △AOB và △COD có:
(cmt)
=> △AOB và △COD là hai tam giác đồng dạng (góc – góc).
=>
Mà: AB = (gt) => => => AO : OC = 1 : 2
Mà AC = AO + OC = 1 + 2 = 3 phần.
=>
- Tương tự với tam giác △BOD và △AOC, suy ra: (bạn trình bày tương tự nhé)
b) Chứng minh EH = HK = KF
Ta đã có các đường:
ME // BD
MF // AC
Do đó:
1. Trong tam giác ABD:
ME // BD ⇒ E là điểm chia BC theo tỉ số: BE : EC = AB : CD = 1:2.
MF // AC ⇒ F là điểm chia AD theo tỉ số : AF : FD = AB : CD = 1 : 2.
Vậy các điểm E, H, K, F nằm trên đoạn EF chia theo cùng tỉ lệ.
- Do MF // AC, giao EF và AC chia đoạn EF theo tỉ số 1 : 2
⇒ H là điểm cách E 1 phần và cách F 2 phần.
- Do ME // BD, giao EF và BD chia đoạn EF theo tỉ số 2 : 1
⇒ K là điểm cách E 2 phần và cách F 1 phần.
=> Trên đoạn EF:
EH = 1 phần,
HK=1 phần,
KF = 1 phần.
=> EH = HK = KF. (đpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13097
Đã trả lời bởi chuyên gia
13097 -
 Đã trả lời bởi chuyên gia
12022
Đã trả lời bởi chuyên gia
12022 -
 Đã trả lời bởi chuyên gia
8825
Đã trả lời bởi chuyên gia
8825 -
 Đã trả lời bởi chuyên gia
6700
Đã trả lời bởi chuyên gia
6700 -
5998