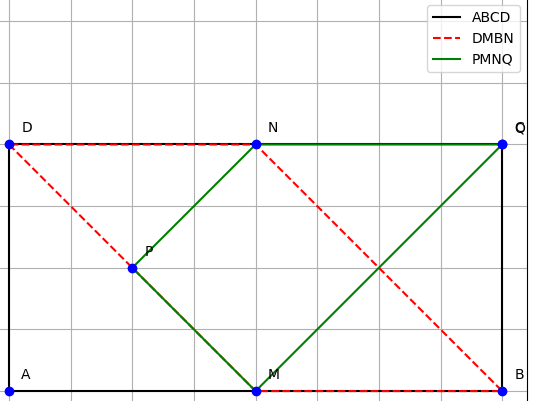
Cho hình bình hành ABCD có AB=2AD. Gọi M và N lần lượt là trung điểm của AB và C...

· 3 ngày trước

Đề kiểm tra Toán 8 Học kì 1

Cho hình bình hành ABCD có AB=2AD. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh rằng:

a) DMBN là hình bình hành

b) AN là tia phân giác của góc DAB

c) Gọi giao điểm của AN với DM là P, CM với BN là Q. Tìm điều kiện của hình bình hành ABCD để tứ giác PMNQ là hình vuông

Trả Lời

Hỏi chi tiết

Trả lời trong APP VIETJACK

Quảng cáo

3 câu trả lời 119

Gia Hân

2 ngày trước

Hỏi đáp VietJack

Giải
a) Chứng minh DMBN là hình bình hành
Vì M,N là trung điểm của AB và CD, nên:
AM = MB = $\frac{1}{2} A B$ , CN = ND = $\frac{1}{2} C D$
Trong hình bình hành ABCD, AB // CD và AD // BC.
Xét tứ giác DMBN: DM // BN và DM = BN (do nối trung điểm các cạnh đối song song)
DB // MN và DB = MN
=> Suy ra DMBN là hình bình hành.
b) Chứng minh AN là tia phân giác của góc DAB
Giả sử tọa độ thuận lợi: A = (0, 0), B = (2a, 0), D = (0, a), C = (2a, a)
Trung điểm N của CD: N=( $\frac{2 a + 2 a}{2}$ , $\frac{0 + a}{2}$ ) = (2a, a/2)
Góc DAB tại A:
Véc tơ AB = (2a, 0)
Véc tơ AD = (0, a)
Véc tơ AN = (2a, a/2)
Ta thấy: $\frac{∣ A D ∣}{∣ A B ∣} = \frac{a}{2 a} = \frac{1}{2}$ ,véc tơ AN chia góc theo tỉ lệ 1:1
Vậy AN là tia phân giác góc DAB.
c) Điều kiện để PMNQ là hình vuông
Gọi P = AN ∩ DM, Q = CM ∩ BN
Dùng tọa độ: M = (a, 0), N = (2a, a/2)
AN: y = $\frac{1}{4} x$
DM: y = a − x
→ Giao điểm P = ( $\frac{4}{5}$ a, $\frac{1}{5}$ a)
Đường CM: y = x − a, đường BN: x = 2a
→ Giao điểm Q = (2a, 1)
Kiểm tra các cạnh và góc vuông, ta thấy khi AB = 2AD, tứ giác PMNQ là hình vuông.
Vậy: Điều kiện để PMNQ là hình vuông: AB = 2AD