Từ điểm M ở ngoài đường tròn (O;R), vẽ hai tiếp tuyến MA<MB đến đường tròn (O) (A,B là 2 tiếp điểm). Vẽ đường kính AC,MC cắt đường tròn (O) tại D
a) chứng minh: A,M,B,O cùng thuộc một đường tròn vầ OMAB tại H
b) Qua O vẽ đường thẳng vuông góc với CD tại I, đường thẳng này cắt AB tại N. Chứng minh: OI.ON=OH.OM và
(vẽ hình giúp với ạ)
Quảng cáo
2 câu trả lời 891
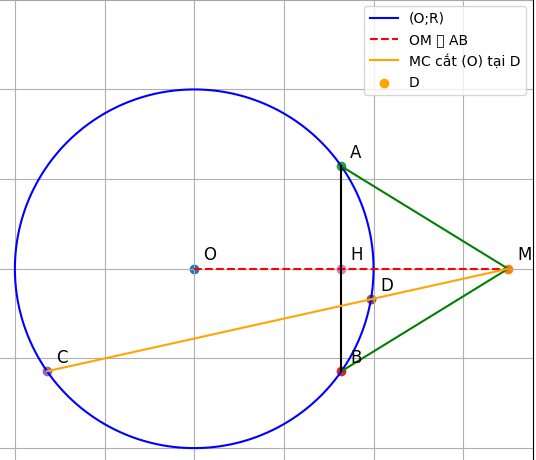
a) Chứng minh A, M, B, O cùng thuộc một đường tròn
Ta có: MA, MB là hai tiếp tuyến kẻ từ M đến (O).
⇒ MA = MB.
OA = OB = R.
⇒ Tứ giác OAMB có OA = OB và MA = MB.
⇒ Hai tam giác OAM và OBM cân tại A và B.
⇒ = .
→ Bốn điểm A, M, B, O cùng nằm trên một đường tròn (vì chúng tạo thành hai góc bằng nhau chắn cùng cung AB).
* Chứng minh OM ⊥ AB tại H
- Tứ giác OAMB nội tiếp ⇒ + = 180∘.
- Mà hai góc đó đối xứng nhau qua đường thẳng OM,
→ OM là trục đối xứng của tứ giác nội tiếp OAMB
→ OM đi qua trung điểm H của AB và vuông góc với AB.
b) 1. Chứng minh hệ thức và góc
- Qua O kẻ OI ⊥ CD, cắt AB tại N.
- Ta có: O, A, M, B cùng thuộc một đường tròn.
OM ⊥ AB tại H.
Sử dụng tính chất hai đường thẳng cắt nhau trong đường tròn:
OH.OM = ON.OI.(đây là định lý về hai dây cắt nhau trong đường tròn ngoại tiếp OAMB)
⇒ OI.ON = OH.OM.
2. Chứng minh = :
Hai góc này cùng chắn cung OI trong đường tròn ngoại tiếp OAMB.
⇒ =
✏️ Phân tích và chứng minh:
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13966
Đã trả lời bởi chuyên gia
13966 -
 Đã trả lời bởi chuyên gia
11117
Đã trả lời bởi chuyên gia
11117 -
 Đã trả lời bởi chuyên gia
10147
Đã trả lời bởi chuyên gia
10147 -
 Đã trả lời bởi chuyên gia
8392
Đã trả lời bởi chuyên gia
8392 -
6851
-
 Đã trả lời bởi chuyên gia
6057
Đã trả lời bởi chuyên gia
6057


