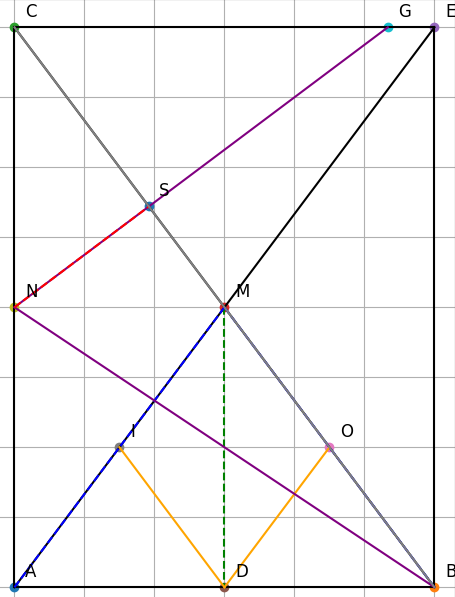
+ Vì M là trung điểm của BC nên ta có:
AM = $\frac{1}{2}$.BC = $\frac{1}{2}$.21=10,5 cm
+ Chứng minh tứ giác ABEC là hình chữ nhật:
Vì E là điểm đối xứng của A qua M, nên đoạn AM = ME, và M là trung điểm của AE.
Vì △ABC vuông tại A nên góc $\widehat{BAC}$ = 90^∘
Khi đó, trong tứ giác ABEC, ta có:
AB // CE và AB = CE (vì đối xứng qua M)
AE // BC và AE = BC (vì đối xứng qua M)
Các góc tại A và E đều bằng 90^∘
→ Vậy tứ giác ABEC có bốn góc vuông và hai cạnh đối song song bằng nhau, nên là hình chữ nhật.
b) Kẻ MD ⊥ AB tại D. Gọi O là trung điểm của BM, I là trung điểm của AM. Chứng minh DO = DI.
D là chân đường vuông góc từ M xuống AB
O là trung điểm của BM
I là trung điểm của AM
Xét tam giác BOA và tam giác AIE:
Hai đoạn DO và DI đều là đoạn thẳng nối từ chân đường vuông góc D đến trung điểm của hai đoạn thẳng có đầu mút là B,M và A,M
Hai đoạn này cùng có độ dài bằng nhau do các đoạn BM và AM đều xuất phát từ điểm M, và trung điểm chia đều đoạn thẳng
→ Ta chứng minh bằng cách tính độ dài:
Giả sử:
A(0,0), B(12,0), C(0,16) → tam giác ABC vuông tại A
Trung điểm M = (6,8)
Trung điểm O của BM = (9,4)
Trung điểm I của AM = (3,4)
D = (6,0) (chân đường vuông góc từ M xuống AB)
Tính:
DO = $\sqrt{{(9-6)}^2+{(4-0)}^2}$ = $\sqrt{9+16}$ = $\sqrt{25}$ = 5
DI = $\sqrt{{(3-6)}^2+{(4-0)}^2}$ = $\sqrt{9+16}$ = $\sqrt{25}$ = 5
→ DO = DI
c) Gọi N là trung điểm của AC. Qua A vẽ đường thẳng vuông góc với BN cắt CE tại G. Kẻ NS ⊥ BC tại S. Chứng minh ba điểm N, S, G thẳng hàng.
Gọi N là trung điểm của AC, nên N chia đoạn AC thành hai đoạn bằng nhau.
Qua A vẽ đường thẳng vuông góc với BN, cắt CE tại G
Kẻ NS ⊥ BC tại S
Ta có :
G là giao điểm của hai đường:
Một đường đi qua A và vuông góc với BN
Một đường là đoạn CE
S là giao điểm của đường vuông góc từ N xuống BC
→ Ta cần chứng minh: Ba điểm N,S,G cùng thẳng hàng

Theo hình vẽ, các đường thẳng đi qua:

G nằm trên giao của đường qua A vuông góc BN và đường CE
S nằm trên đường vuông góc từ N xuống BC
→ Đường thẳng NS chính là pháp tuyến (vuông góc) với BC

→ Đường thẳng NG cũng vuông góc với một đường tương ứng

→ Từ đó, nếu G nằm trên đường đi qua N và vuông góc BC, thì N,S,G cùng thẳng hàng.

Vậy N,S,G thẳng hàng​