cho tam giác ABC vuông tại A (AB<AC),đường cao AH,trung tuyến AM. Lấy điểm P sao cho M là trung điểm của đoạn thẳng AP
a) ABPC là hình chữ nhật (giải rồi)
b) Kẻ PR vuông góc với BC. Chứng minh rằng tứ giác AHPR là hình bình hành và M là trung điểm HR
Quảng cáo
3 câu trả lời 861
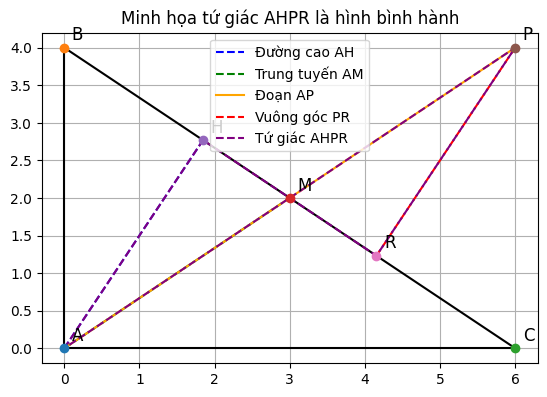
1. Chứng minh tứ giác AHPR là hình bình hành
+ Xét tứ giác AHPR:
Có AH ⊥ BC, mà PR ⊥ BC (cùng vuông góc với BC)
→ AH // PR
+ Xét hai điểm A và P, ta có:
M là trung điểm của AP
M cũng là trung điểm của HR (sẽ chứng minh ở phần sau)
→ Suy ra: AHPR có hai cạnh đối vừa song song vừa bằng nhau, đó là:
AH // PR và AH = PR
+ Vậy AHPR là hình bình hành.
2. Chứng minh M là trung điểm của đoạn thẳng HR
Vì M là trung điểm của AP (giả thiết)
+ Hình bình hành AHPR → AC và PR cắt nhau tại trung điểm mỗi cạnh
→ Trong hình bình hành, giao điểm của hai đường chéo là trung điểm của mỗi đường chéo
→ Vậy:
M là trung điểm của HR
phần a giả r thì phần b
phần b)
AHPR là hình bình hành vì:
AH ∥ PR ,AH=PR
Là giao điểm của hai đường chéo trong hình bình hành
Tứ giác AHPRlà hình bình hành vì có 2 cặp cạnh đối song song và bằng nhau.
M là trung điểm của HR vì nó là trung điểm của AP và AP=HR
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12687
Đã trả lời bởi chuyên gia
12687 -
 Đã trả lời bởi chuyên gia
11433
Đã trả lời bởi chuyên gia
11433 -
9813
-
 Đã trả lời bởi chuyên gia
5661
Đã trả lời bởi chuyên gia
5661 -
 Đã trả lời bởi chuyên gia
5337
Đã trả lời bởi chuyên gia
5337


