Tam giác ABC vuông ở A. H bất kì ở giữa B và C
Kẻ HI vuông góc AB tại I. Lấy D đối xứng với H qua I
Kẻ HK vuông góc AC tại K. Lấy E đối xứng với H qua K
Chứng minh rằng: A,D,E thẳng hàng
Quảng cáo
3 câu trả lời 213
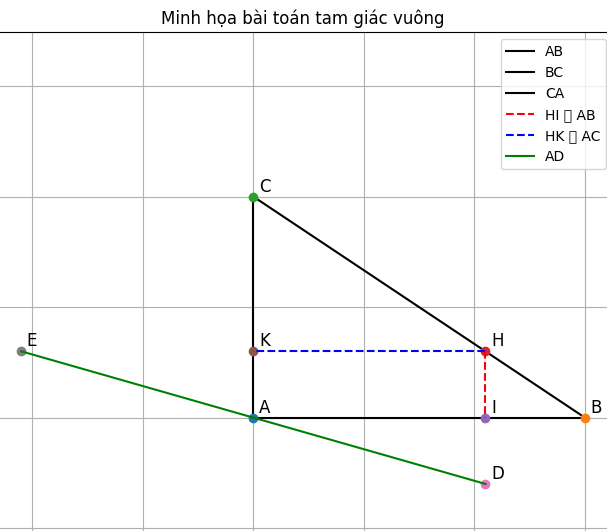
+ Vì tam giác ABC vuông tại A, ta có: AB AC
+ Xét các đường vuông góc
HI AB tại I ⇒ I là hình chiếu vuông góc của H lên AB
HK AC tại K ⇒ K là hình chiếu vuông góc của H lên AC
+ Đối xứng qua I và K
D là điểm đối xứng của H qua I ⇒ I là trung điểm của đoạn HD
E là điểm đối xứng của H qua K ⇒ K là trung điểm của đoạn HE
⇒ Hai điểm D và E nằm đối xứng với nhau qua hai đường vuông góc tại A
+ Ta xét tam giác DHE, trong đó:
I là trung điểm của HD
K là trung điểm của HE
HI AB, HK AC, mà AB AC
⇒ Hai đường HI và HK vuông góc với hai cạnh vuông góc tại A, nên đường nối D và E sẽ đi qua điểm A
-
Bước 1: Xác định các điểm và tính chất của tam giác
- Tam giác ABC vuông tại A, nghĩa là
- H là điểm bất kỳ nằm giữa B và C.
- I là giao điểm của HI với AB, và HI vuông góc với AB.
- D là điểm đối xứng của H qua I.
- K là giao điểm của HK với AC, và HK vuông góc với AC.
- E là điểm đối xứng của H qua K.
-
Bước 2: Tính chất đối xứng
- Vì D là điểm đối xứng của H qua I, nên ta có:
- Tương tự, vì E là điểm đối xứng của H qua K, nên:
- Vì D là điểm đối xứng của H qua I, nên ta có:
-
Bước 3: Xét các tam giác
- Xét tam giác HIK và tam giác DKI:
- Tam giác HIK vuông tại I (vì HI vuông góc với AB).
- Tam giác DKI cũng vuông tại I (vì DI = HI và HI vuông góc với AB).
- Xét tam giác HIK và tam giác DKI:
-
Bước 4: Sử dụng tính chất vuông góc
- Vì HK vuông góc với AC, nên ta có:
- Tương tự, ta có:
-
Bước 5: Kết luận
- Từ các tính chất trên, ta thấy rằng A, D, E đều nằm trên một đường thẳng vì:
- D và E đều được xác định từ H qua các điểm I và K, và đều có cùng một góc vuông với AC.
- Do đó, A, D, E thẳng hàng.
- Từ các tính chất trên, ta thấy rằng A, D, E đều nằm trên một đường thẳng vì:
Kết luận:
A, D, E thẳng hàng.
Cho tam giác vuông △ABC\triangle ABC△ABC vuông tại A, điểm HHH nằm giữa BBB và CCC.
Kẻ HI⊥ABHI \perp ABHI⊥AB tại III, lấy DDD là điểm đối xứng của HHH qua III.
Kẻ HK⊥ACHK \perp ACHK⊥AC tại KKK, lấy EEE là điểm đối xứng của HHH qua KKK.
Kết luận: A,D,EA, D, EA,D,E thẳng hàng. ✅
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
17097
Đã trả lời bởi chuyên gia
17097 -
 Đã trả lời bởi chuyên gia
16079
Đã trả lời bởi chuyên gia
16079 -
 Đã trả lời bởi chuyên gia
10012
Đã trả lời bởi chuyên gia
10012 -
 Đã trả lời bởi chuyên gia
8884
Đã trả lời bởi chuyên gia
8884 -
 Đã trả lời bởi chuyên gia
8830
Đã trả lời bởi chuyên gia
8830 -
 Đã trả lời bởi chuyên gia
7498
Đã trả lời bởi chuyên gia
7498 -
 Đã trả lời bởi chuyên gia
5904
Đã trả lời bởi chuyên gia
5904


