Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a) Tứ giác BMNC là hình gì ? Vì sao ?
b) Tính các góc của tứ giác BMNC biết rằng A = 40°.
Quảng cáo
3 câu trả lời 208
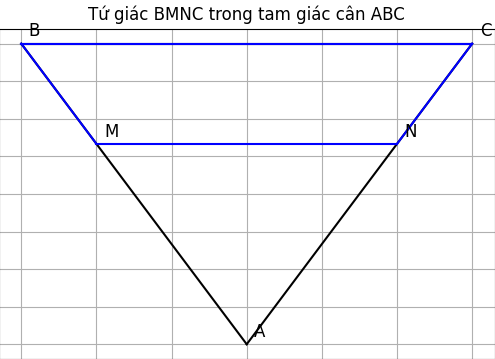
a) Vì tam giác ABC cân tại A nên:
AB = AC và =
Gọi điểm M ∈ AB, N ∈ AC sao cho:
BM = CN(giả thiết)
Xét △CBM và △BCN, ta có:
Cạnh CB chung
= (tam giác cân tại A)
BM = CN (giả thiết)
⇒△CBM = △BCN (c.g.c)
⇒ =
Suy ra, trong tứ giác BMNC, hai góc đáy bằng nhau, hai cạnh bên BM = CN.
⇒BMNC là hình thang cân
b) Trong tam giác cân ABC, ta có:
+ = 180∘ − = 180∘ − 40∘ = 140∘
⇒ = = 1 = 70∘
Tứ giác BMNC là hình thang cân, nên:
Hai góc tại đỉnh B và C: = = 70∘
=> Hai góc còn lại: 4 = 5 = 180∘ − 70∘ = 110∘
Các góc của tứ giác BMNC là ∠B=70∘
, ∠C=70∘angle cap C equals 70 raised to the composed with power
∠𝐶=70∘, ∠M=110∘
, ∠N=110∘
.
...
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12666
Đã trả lời bởi chuyên gia
12666 -
 Đã trả lời bởi chuyên gia
11411
Đã trả lời bởi chuyên gia
11411 -
9654
-
 Đã trả lời bởi chuyên gia
5640
Đã trả lời bởi chuyên gia
5640 -
 Đã trả lời bởi chuyên gia
5324
Đã trả lời bởi chuyên gia
5324


