cho các số thực dương x,y,z thỏa mãn x+y+z=3 chứng minh 1x2+x+1y2+y++1z2+z...

Question

cho các số thực dương x,y,z thỏa mãn x+y+z=3 chứng minh 1x2+x+1y2+y++1z2+z≥32

VietJack · Accepted Answer

Xem đáp án từ VietJack...

VietJack · Answer

Dấu bằng xảy ra khi x=y=z=1 .

VietJack · Answer

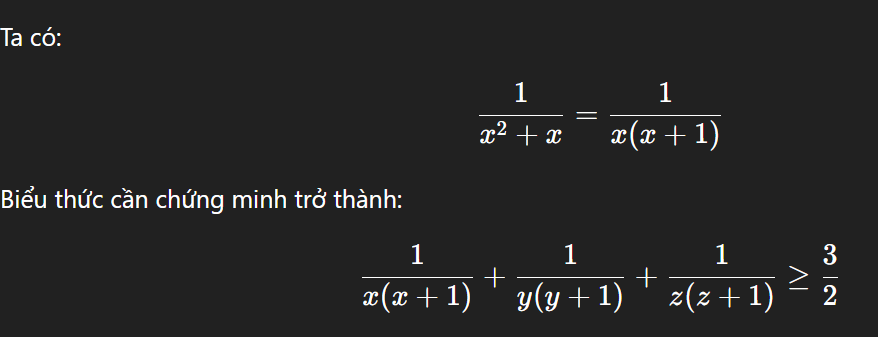
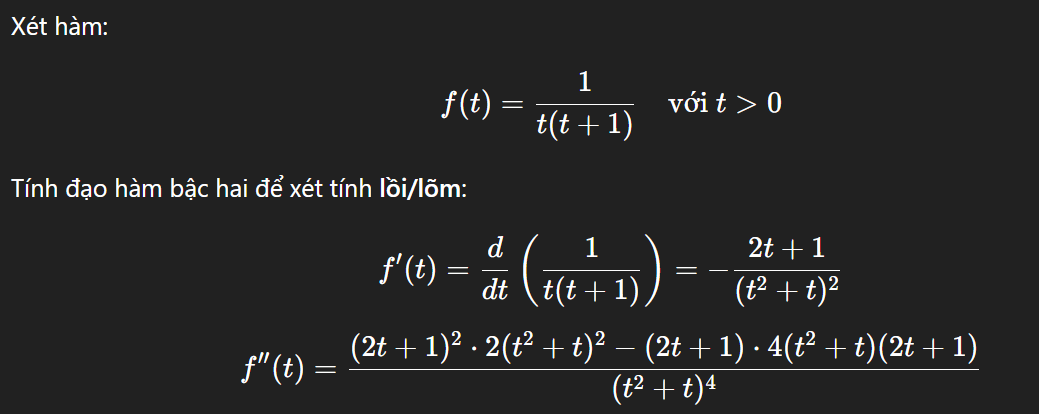
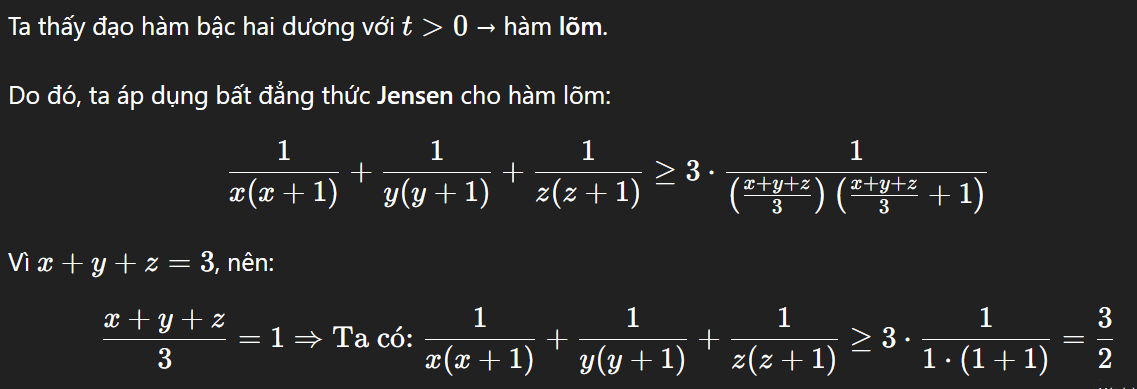
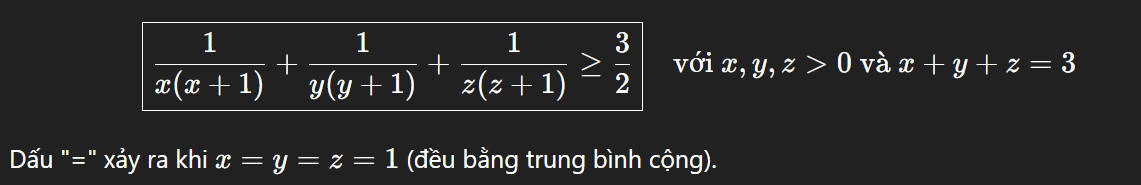
thường là tại x=y=z=1. Khi đó, vế trái của bất đẳng thức bằng:

12+1+11+12+1+11+12+1+11=31+31+31=1

Vì 1<23, nên bất đẳng thức ban đầu là sai. Một dạng đề phổ biến và đúng của bài toán này là chứng minh vế trái lớn hơn hoặc bằng 1.

Dưới đây là lời giải cho bất đẳng thức đúng: Chứng minh: x2+x+11+y2+y+11+z2+z+11≥1

Chứng Minh Bất Đẳng Thức Phụ
Để giải quyết bài toán, ta sẽ sử dụng một bất đẳng thức phụ rất mạnh và hữu ích. Ta chứng minh rằng với mọi số thực dương a, ta có:

a2+a+11≥32−a
Chứng minh bất đẳng thức phụ: Biến đổi tương đương, ta có: a2+a+11−32−a≥0

Quy đồng mẫu số và rút gọn vế trái: 3(a2+a+1)3−(2−a)(a2+a+1)≥0

Xét tử số: 3−(2a2+2a+2−a3−a2−a) =3−(a2+a+2−a3) =a3−a2−a+1 =a2(a−1)−(a−1) =(a2−1)(a−1) =(a−1)(a+1)(a−1) =(a−1)2(a+1)

Do đó, bất đẳng thức tương đương với:

3(a2+a+1)(a−1)2(a+1)≥0
Vì a là số thực dương nên a>0, suy ra a+1>0 và a2+a+1>0. Hơn nữa, (a−1)2≥0. Vậy, bất đẳng thức luôn đúng. Dấu "=" xảy ra khi và chỉ khi a−1=0⟹a=1.

Áp Dụng Bất Đẳng Thức

Áp dụng bất đẳng thức phụ đã chứng minh cho các biến x,y,z, ta có:

x2+x+11≥32−x
y2+y+11≥32−y
z2+z+11≥32−z
Cộng ba bất đẳng thức trên vế theo vế, ta được:

x2+x+11+y2+y+11+z2+z+11≥32−x+32−y+32−z
≥3(2−x)+(2−y)+(2−z)=36−(x+y+z)
Theo giả thiết, ta có x+y+z=3. Thay vào biểu thức trên:

36−3=33=1
Vậy, ta đã chứng minh được:

x2+x+11+y2+y+11+z2+z+11≥1
Dấu "=" xảy ra khi và chỉ khi x=y=z=1.

...Xem thêm

VietJack · Answer

$ dfrac{1}{x^2 + x} + dfrac{1}{y^2 + y} + dfrac{1}{z^2 + z}$ $= dfrac{1}{x(x + 1)} + dfrac{1}{y(y + 1)} + dfrac{1}{z(z + 1)}$ $= dfrac{1}{x} - dfrac{1}{x + 1} + dfrac{1}{y} - dfrac{1}{y + 1} + dfrac{1}{z} - dfrac{1}{z + 1}$ Đặt $A = dfrac{1}{x} - dfrac{1}{x + 1} + dfrac{1}{y} - dfrac{1}{y + 1} + dfrac{1}{z} - dfrac{1}{z + 1}$ Áp dụng BĐT Cauchy - Schwarz, ta có: $ dfrac{1}{x} + dfrac{1}{1} ge dfrac{4}{x + 1}$ $ dfrac{1}{y} + dfrac{1}{1} ge dfrac{4}{y + 1}$ $ dfrac{1}{z} + dfrac{1}{1} ge dfrac{4}{z + 1}$ Suy ra $A ge dfrac{4}{x + 1} - 1 - dfrac{1}{x + 1} + dfrac{4}{y + 1} - 1 - dfrac{1}{y + 1} + dfrac{4}{z + 1} - 1 - dfrac{1}{z + 1}$ Hay $A ge dfrac{3}{x + 1} + dfrac{3}{y + 1} + dfrac{3}{z + 1} - 3$ Áp dụng BĐT Cauchy - Schwarz, ta có: $ dfrac{1}{x + 1} + dfrac{1}{y + 1} + dfrac{1}{z + 1} ge dfrac{9}{x + y + z + 3}$ Suy ra $A ge dfrac{27}{x +y + z + 3} - 3 = dfrac{27}{3 + 3} - 3 = dfrac{3}{2}$ Dấu $=$ xảy ra khi $x = y = z = 1$ Vậy bất đẳng thức đã được chứng minh

4 câu trả lời 163

Câu hỏi hot cùng chủ đề

Bài viết mới nhất Lớp 9