Cho tam giác ABC vuông tại A. Kẻ phân giác BD của góc ABC (D thuộc AC) Từ D kẻ DE vuông góc với BC tại E
a) CMinh tam giác ABD = tam giác EBD
b) BD trung trực của AE
(Được thêm hình vẽ của tam giác nữa thì tốt ạ)
Quảng cáo
4 câu trả lời 254
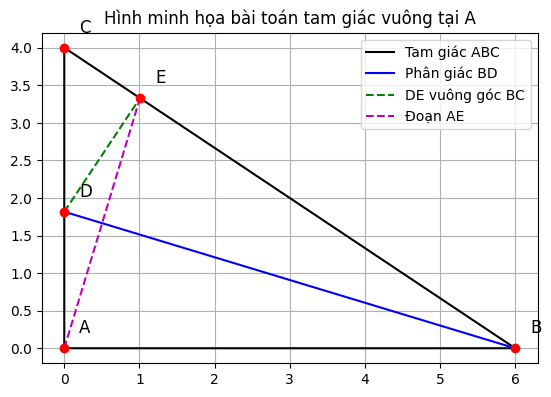
Xét hai tam giác △ABD và △EBD:
Có cạnh chung: BD
= (vì BD là phân giác của )
AD = DE (vì tam giác vuông tại A, và DE vuông góc hạ từ D lên BC → sẽ chứng minh bằng tam giác vuông sau)
=> Hai tam giác ABD và EBD có hai cạnh và góc xen giữa bằng nhau.
=> △ABD = △EBD(c.g.c)
b, Chứng minh BD là trung trực của AE
Từ phần (a), có: △ABD = △EBD
=> AB = EB
AD = DE
→ AE là đoạn thẳng nối hai điểm đối xứng qua đường BD
→ BD vuông góc và chia đôi AE
=> BD ⊥ AE và BD đi qua trung điểm của AE
⇒BD là trung trực của AE (đpcm)
), và điểm D cách đều A và E ( AD=ED
).
4. Theo tính chất đường trung trực, đường thẳng đi qua hai điểm cách đều hai đầu đoạn thẳng là đường trung trực của đoạn thẳng đó.
5. Vậy, BD
là đường trung trực của AE
TG ABD=TG CBD(ch-cgn)
Ta có:
TG ABD= TG EBD(cgc)
=>AE=ED( cạnh tương ứng)
BA=BE(cạnh tương ứng)
=>BD là đường trung tuyến TG ABE
Xét TG ABE có:
BA=BE(cmt)
=>TG ABE là TG cân
=> BD đồng thời là đường trung trực
=> đpcm
*TG là tam giác nhé
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
12233
-
5721
-
4825


