Đã trả lời bởi chuyên gia
Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. Gọi M và N theo thứ tự là hình chiếu của E và D trện BC. a) Chứng minh tỉ số khoảng cách từ H đến EM và DN bằng EM DN b) Gọi O là giao điểm của DM và EN. Chứng minh Họ vuông góc với BC
Quảng cáo
4 câu trả lời 2426
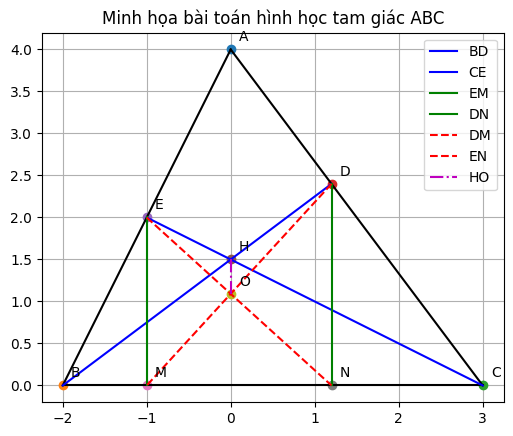
a, Ta có :
D ∈ AC, E ∈ ABE , do là chân đường cao từ B,C
M, N là hình chiếu vuông góc từ E, D lên BC
Do đó:
EM ⊥ BC, DN ⊥ BC
⇒ EM // DN
+ Xét hai tam giác △HEM và △HDN có :
Cạnh đáy EM // DN
Đỉnh chung là H
Cùng nằm giữa hai đường thẳng song song EM, DN
Đỉnh chung là H
Cùng nằm giữa hai đường thẳng song song EM, DN
Cả hai tam giác HEM và HDN đều nằm giữa hai đường song song EM và DN, và có chân đường cao nằm trên cùng đường thẳng BC.
Khoảng cách từ H đến EM bằng khoảng cách từ H đến DN
Vì EM // DN, nên các chiều cao này bằng nhau
⟹ Hai tam giác HEM và HDN có cùng chiều cao, lại có đáy bằng nhau khi so tỉ lệ (như hình phản chiếu nhau)
=> SHEM=SHDN
=> (vì tỷ số nghịch đảo)
=> (đpcm)
b, Xét phép đối xứng trục qua đường thẳng BC:
E ↦ ME : do MMM là hình chiếu của EEE qua đường vuông góc với BCBCBC
D ↦ ND: tương tự
Vì vậy, điểm O = DM ∩ EN là tâm đối xứng của đoạn thẳng ED qua trục BC
⟹ Đoạn thẳng HO sẽ vuông góc với trục đối xứng nếu H đối xứng với chính nó, hoặc nằm trên đường vuông góc kẻ từ O đến BC
+ Tam giác đồng dạng và trực tâm
Ta cũng có thể dùng góc:
EM ⊥ BC, DN ⊥ BC ⇒ EM // DN
Hai đường DM và EN cắt nhau tại O, tạo thành hai tam giác nhỏ: △DMO, △ENO
Chúng đối xứng nhau qua trục vuông góc với BC, nên:
HO là đường trung trực của đoạn DE
Mà D, E thuộc hai đường cao xuất phát từ đỉnh B, C
⇒ H cũng nằm trên đường vuông góc này
⟹ HO ⊥ BC (đpcm)
Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. Gọi M và N theo thứ tự là hình chiếu của E và D trên BC.
a) Chứng minh tỉ số khoảng cách từ H đến EM và DN bằng EM/DN:
Gọi khoảng cách từ H đến EM là x, khoảng cách từ H đến DN là y.
Ta có:
Tam giác BDC vuông tại D nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
.
Tam giác BEC vuông tại E nên CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
.
Xét tứ giác DMEN, ta có: ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Vì ME//NDcap M cap E / / cap N cap D
??//??
và BD,CEcap B cap D comma cap C cap E
??,??
là đường cao nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
, CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
. Do đó, tứ giác DMEN là hình thang vuông tại M và N.
Tam giác BEC vuông tại E có EM là đường cao, nên EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Tam giác BDC vuông tại D có DN là đường cao, nên DN2=BN.NCcap D cap N squared equals cap B cap N point cap N cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Xét tam giác BHC có HM⟂BCcap H cap M ⟂ cap B cap C
??⟂??
và HN⟂BCcap H cap N ⟂ cap B cap C
??⟂??
, nên HM=xcap H cap M equals x
??=?
và HN=ycap H cap N equals y
??=?
.
Xét tam giác BEC vuông tại E có EM là đường cao, nên BM.BC=BE2cap B cap M point cap B cap C equals cap B cap E squared
??.??=??2
và EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
.
Xét tam giác BDC vuông tại D có DN là đường cao, nên CN.BC=CD2cap C cap N point cap B cap C equals cap C cap D squared
??.??=??2
và DN2=CN.BNcap D cap N squared equals cap C cap N point cap B cap N
??2=??.??
.
Xét tam giác vuông BHD, ta có BH2=BD2+DH2cap B cap H squared equals cap B cap D squared plus cap D cap H squared
??2=??2+??2
và DH2=BN.BCcap D cap H squared equals cap B cap N point cap B cap C
??2=??.??
.
Xét tam giác vuông CHE, ta có CH2=CE2+HE2cap C cap H squared equals cap C cap E squared plus cap H cap E squared
??2=??2+??2
và HE2=CM.CBcap H cap E squared equals cap C cap M point cap C cap B
??2=??.??
.
Vì H là trực tâm của tam giác ABC nên BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có xy=HMHN=EMDNx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????=????
.
Vì ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tam giác HME và tam giác HDN đồng dạng (g-g).
xy=HMHN=HEHDx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap H cap E and denominator cap H cap D end-fraction
??=????=????
.
Ta có HEHD=CMBDthe fraction with numerator cap H cap E and denominator cap H cap D end-fraction equals the fraction with numerator cap C cap M and denominator cap B cap D end-fraction
????=????
.
Vì EM⟂BCcap E cap M ⟂ cap B cap C
??⟂??
và DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
nên EM//DNcap E cap M / / cap D cap N
??//??
.
Do đó HMHN=EMDNthe fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
????=????
.
Vậy, xy=EMDNx over y end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????
.
b) Gọi O là giao điểm của DM và EN. Chứng minh HO vuông góc với BC:
Gọi I là giao điểm của DM và EN.
Xét tứ giác DMEN, ta có ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
, suy ra ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó tứ giác DMEN là hình thang.
Vì O là giao điểm của DM và EN nên O là giao điểm của hai đường chéo của hình thang DMEN.
Do O là giao điểm của hai đường chéo của hình thang DMEN nên O là trung điểm của MN.
Gọi H là trực tâm của tam giác ABC, ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có EM là đường cao của tam giác BEC nên ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
.
Ta có DN là đường cao của tam giác BDC nên DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
.
Vì vậy, ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tứ giác DMEN là hình thang.
Gọi I là giao điểm của DM và EN. Ta có I là giao điểm của hai đường chéo của hình thang DMEN.
Gọi H là trực tâm tam giác ABC, thì Hcap H
?
thuộc BDcap B cap D
??
và Hcap H
?
thuộc CEcap C cap E
??
.
Vì BD⟂ACcap B cap D ⟂ cap A cap C
??⟂??
và CE⟂ABcap C cap E ⟂ cap A cap B
??⟂??
nên Hcap H
?
là trực tâm của tam giác ABC.
O là giao điểm của DM và EN, ta có O là giao điểm hai đường chéo của hình thang DMEN.
a) Chứng minh tỉ số khoảng cách từ H đến EM và DN bằng EM/DN:
Gọi khoảng cách từ H đến EM là x, khoảng cách từ H đến DN là y.
Ta có:
Tam giác BDC vuông tại D nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
.
Tam giác BEC vuông tại E nên CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
.
Xét tứ giác DMEN, ta có: ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Vì ME//NDcap M cap E / / cap N cap D
??//??
và BD,CEcap B cap D comma cap C cap E
??,??
là đường cao nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
, CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
. Do đó, tứ giác DMEN là hình thang vuông tại M và N.
Tam giác BEC vuông tại E có EM là đường cao, nên EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Tam giác BDC vuông tại D có DN là đường cao, nên DN2=BN.NCcap D cap N squared equals cap B cap N point cap N cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Xét tam giác BHC có HM⟂BCcap H cap M ⟂ cap B cap C
??⟂??
và HN⟂BCcap H cap N ⟂ cap B cap C
??⟂??
, nên HM=xcap H cap M equals x
??=?
và HN=ycap H cap N equals y
??=?
.
Xét tam giác BEC vuông tại E có EM là đường cao, nên BM.BC=BE2cap B cap M point cap B cap C equals cap B cap E squared
??.??=??2
và EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
.
Xét tam giác BDC vuông tại D có DN là đường cao, nên CN.BC=CD2cap C cap N point cap B cap C equals cap C cap D squared
??.??=??2
và DN2=CN.BNcap D cap N squared equals cap C cap N point cap B cap N
??2=??.??
.
Xét tam giác vuông BHD, ta có BH2=BD2+DH2cap B cap H squared equals cap B cap D squared plus cap D cap H squared
??2=??2+??2
và DH2=BN.BCcap D cap H squared equals cap B cap N point cap B cap C
??2=??.??
.
Xét tam giác vuông CHE, ta có CH2=CE2+HE2cap C cap H squared equals cap C cap E squared plus cap H cap E squared
??2=??2+??2
và HE2=CM.CBcap H cap E squared equals cap C cap M point cap C cap B
??2=??.??
.
Vì H là trực tâm của tam giác ABC nên BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có xy=HMHN=EMDNx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????=????
.
Vì ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tam giác HME và tam giác HDN đồng dạng (g-g).
xy=HMHN=HEHDx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap H cap E and denominator cap H cap D end-fraction
??=????=????
.
Ta có HEHD=CMBDthe fraction with numerator cap H cap E and denominator cap H cap D end-fraction equals the fraction with numerator cap C cap M and denominator cap B cap D end-fraction
????=????
.
Vì EM⟂BCcap E cap M ⟂ cap B cap C
??⟂??
và DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
nên EM//DNcap E cap M / / cap D cap N
??//??
.
Do đó HMHN=EMDNthe fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
????=????
.
Vậy, xy=EMDNx over y end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????
.
b) Gọi O là giao điểm của DM và EN. Chứng minh HO vuông góc với BC:
Gọi I là giao điểm của DM và EN.
Xét tứ giác DMEN, ta có ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
, suy ra ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó tứ giác DMEN là hình thang.
Vì O là giao điểm của DM và EN nên O là giao điểm của hai đường chéo của hình thang DMEN.
Do O là giao điểm của hai đường chéo của hình thang DMEN nên O là trung điểm của MN.
Gọi H là trực tâm của tam giác ABC, ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có EM là đường cao của tam giác BEC nên ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
.
Ta có DN là đường cao của tam giác BDC nên DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
.
Vì vậy, ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tứ giác DMEN là hình thang.
Gọi I là giao điểm của DM và EN. Ta có I là giao điểm của hai đường chéo của hình thang DMEN.
Gọi H là trực tâm tam giác ABC, thì Hcap H
?
thuộc BDcap B cap D
??
và Hcap H
?
thuộc CEcap C cap E
??
.
Vì BD⟂ACcap B cap D ⟂ cap A cap C
??⟂??
và CE⟂ABcap C cap E ⟂ cap A cap B
??⟂??
nên Hcap H
?
là trực tâm của tam giác ABC.
O là giao điểm của DM và EN, ta có O là giao điểm hai đường chéo của hình thang DMEN.
Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. Gọi M và N theo thứ tự là hình chiếu của E và D trên BC.
a) Chứng minh tỉ số khoảng cách từ H đến EM và DN bằng EM/DN:
Gọi khoảng cách từ H đến EM là x, khoảng cách từ H đến DN là y.
Ta có:
Tam giác BDC vuông tại D nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
.
Tam giác BEC vuông tại E nên CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
.
Xét tứ giác DMEN, ta có: ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Vì ME//NDcap M cap E / / cap N cap D
??//??
và BD,CEcap B cap D comma cap C cap E
??,??
là đường cao nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
, CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
. Do đó, tứ giác DMEN là hình thang vuông tại M và N.
Tam giác BEC vuông tại E có EM là đường cao, nên EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Tam giác BDC vuông tại D có DN là đường cao, nên DN2=BN.NCcap D cap N squared equals cap B cap N point cap N cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Xét tam giác BHC có HM⟂BCcap H cap M ⟂ cap B cap C
??⟂??
và HN⟂BCcap H cap N ⟂ cap B cap C
??⟂??
, nên HM=xcap H cap M equals x
??=?
và HN=ycap H cap N equals y
??=?
.
Xét tam giác BEC vuông tại E có EM là đường cao, nên BM.BC=BE2cap B cap M point cap B cap C equals cap B cap E squared
??.??=??2
và EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
.
Xét tam giác BDC vuông tại D có DN là đường cao, nên CN.BC=CD2cap C cap N point cap B cap C equals cap C cap D squared
??.??=??2
và DN2=CN.BNcap D cap N squared equals cap C cap N point cap B cap N
??2=??.??
.
Xét tam giác vuông BHD, ta có BH2=BD2+DH2cap B cap H squared equals cap B cap D squared plus cap D cap H squared
??2=??2+??2
và DH2=BN.BCcap D cap H squared equals cap B cap N point cap B cap C
??2=??.??
.
Xét tam giác vuông CHE, ta có CH2=CE2+HE2cap C cap H squared equals cap C cap E squared plus cap H cap E squared
??2=??2+??2
và HE2=CM.CBcap H cap E squared equals cap C cap M point cap C cap B
??2=??.??
.
Vì H là trực tâm của tam giác ABC nên BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có xy=HMHN=EMDNx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????=????
.
Vì ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tam giác HME và tam giác HDN đồng dạng (g-g).
xy=HMHN=HEHDx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap H cap E and denominator cap H cap D end-fraction
??=????=????
.
Ta có HEHD=CMBDthe fraction with numerator cap H cap E and denominator cap H cap D end-fraction equals the fraction with numerator cap C cap M and denominator cap B cap D end-fraction
????=????
.
Vì EM⟂BCcap E cap M ⟂ cap B cap C
??⟂??
và DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
nên EM//DNcap E cap M / / cap D cap N
??//??
.
Do đó HMHN=EMDNthe fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
????=????
.
Vậy, xy=EMDNx over y end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????
.
b) Gọi O là giao điểm của DM và EN. Chứng minh HO vuông góc với BC:
Gọi I là giao điểm của DM và EN.
Xét tứ giác DMEN, ta có ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
, suy ra ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó tứ giác DMEN là hình thang.
Vì O là giao điểm của DM và EN nên O là giao điểm của hai đường chéo của hình thang DMEN.
Do O là giao điểm của hai đường chéo của hình thang DMEN nên O là trung điểm của MN.
Gọi H là trực tâm của tam giác ABC, ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có EM là đường cao của tam giác BEC nên ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
.
Ta có DN là đường cao của tam giác BDC nên DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
.
Vì vậy, ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tứ giác DMEN là hình thang.
Gọi I là giao điểm của DM và EN. Ta có I là giao điểm của hai đường chéo của hình thang DMEN.
Gọi H là trực tâm tam giác ABC, thì Hcap H
?
thuộc BDcap B cap D
??
và Hcap H
?
thuộc CEcap C cap E
??
.
Vì BD⟂ACcap B cap D ⟂ cap A cap C
??⟂??
và CE⟂ABcap C cap E ⟂ cap A cap B
??⟂??
nên Hcap H
?
là trực tâm của tam giác ABC.
O là giao điểm của DM và EN, ta có O là giao điểm hai đường chéo của hình thang DMEN.
...Xem thêm
a) Chứng minh tỉ số khoảng cách từ H đến EM và DN bằng EM/DN:
Gọi khoảng cách từ H đến EM là x, khoảng cách từ H đến DN là y.
Ta có:
Tam giác BDC vuông tại D nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
.
Tam giác BEC vuông tại E nên CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
.
Xét tứ giác DMEN, ta có: ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Vì ME//NDcap M cap E / / cap N cap D
??//??
và BD,CEcap B cap D comma cap C cap E
??,??
là đường cao nên BD⟂BCcap B cap D ⟂ cap B cap C
??⟂??
, CE⟂BCcap C cap E ⟂ cap B cap C
??⟂??
. Do đó, tứ giác DMEN là hình thang vuông tại M và N.
Tam giác BEC vuông tại E có EM là đường cao, nên EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Tam giác BDC vuông tại D có DN là đường cao, nên DN2=BN.NCcap D cap N squared equals cap B cap N point cap N cap C
??2=??.??
(hệ thức lượng trong tam giác vuông).
Ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Xét tam giác BHC có HM⟂BCcap H cap M ⟂ cap B cap C
??⟂??
và HN⟂BCcap H cap N ⟂ cap B cap C
??⟂??
, nên HM=xcap H cap M equals x
??=?
và HN=ycap H cap N equals y
??=?
.
Xét tam giác BEC vuông tại E có EM là đường cao, nên BM.BC=BE2cap B cap M point cap B cap C equals cap B cap E squared
??.??=??2
và EM2=BM.MCcap E cap M squared equals cap B cap M point cap M cap C
??2=??.??
.
Xét tam giác BDC vuông tại D có DN là đường cao, nên CN.BC=CD2cap C cap N point cap B cap C equals cap C cap D squared
??.??=??2
và DN2=CN.BNcap D cap N squared equals cap C cap N point cap B cap N
??2=??.??
.
Xét tam giác vuông BHD, ta có BH2=BD2+DH2cap B cap H squared equals cap B cap D squared plus cap D cap H squared
??2=??2+??2
và DH2=BN.BCcap D cap H squared equals cap B cap N point cap B cap C
??2=??.??
.
Xét tam giác vuông CHE, ta có CH2=CE2+HE2cap C cap H squared equals cap C cap E squared plus cap H cap E squared
??2=??2+??2
và HE2=CM.CBcap H cap E squared equals cap C cap M point cap C cap B
??2=??.??
.
Vì H là trực tâm của tam giác ABC nên BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có xy=HMHN=EMDNx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????=????
.
Vì ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
nên ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tam giác HME và tam giác HDN đồng dạng (g-g).
xy=HMHN=HEHDx over y end-fraction equals the fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap H cap E and denominator cap H cap D end-fraction
??=????=????
.
Ta có HEHD=CMBDthe fraction with numerator cap H cap E and denominator cap H cap D end-fraction equals the fraction with numerator cap C cap M and denominator cap B cap D end-fraction
????=????
.
Vì EM⟂BCcap E cap M ⟂ cap B cap C
??⟂??
và DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
nên EM//DNcap E cap M / / cap D cap N
??//??
.
Do đó HMHN=EMDNthe fraction with numerator cap H cap M and denominator cap H cap N end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
????=????
.
Vậy, xy=EMDNx over y end-fraction equals the fraction with numerator cap E cap M and denominator cap D cap N end-fraction
??=????
.
b) Gọi O là giao điểm của DM và EN. Chứng minh HO vuông góc với BC:
Gọi I là giao điểm của DM và EN.
Xét tứ giác DMEN, ta có ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
và ND⟂BCcap N cap D ⟂ cap B cap C
??⟂??
, suy ra ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó tứ giác DMEN là hình thang.
Vì O là giao điểm của DM và EN nên O là giao điểm của hai đường chéo của hình thang DMEN.
Do O là giao điểm của hai đường chéo của hình thang DMEN nên O là trung điểm của MN.
Gọi H là trực tâm của tam giác ABC, ta có BH⟂ACcap B cap H ⟂ cap A cap C
??⟂??
và CH⟂ABcap C cap H ⟂ cap A cap B
??⟂??
.
Ta có EM là đường cao của tam giác BEC nên ME⟂BCcap M cap E ⟂ cap B cap C
??⟂??
.
Ta có DN là đường cao của tam giác BDC nên DN⟂BCcap D cap N ⟂ cap B cap C
??⟂??
.
Vì vậy, ME//NDcap M cap E / / cap N cap D
??//??
.
Do đó, tứ giác DMEN là hình thang.
Gọi I là giao điểm của DM và EN. Ta có I là giao điểm của hai đường chéo của hình thang DMEN.
Gọi H là trực tâm tam giác ABC, thì Hcap H
?
thuộc BDcap B cap D
??
và Hcap H
?
thuộc CEcap C cap E
??
.
Vì BD⟂ACcap B cap D ⟂ cap A cap C
??⟂??
và CE⟂ABcap C cap E ⟂ cap A cap B
??⟂??
nên Hcap H
?
là trực tâm của tam giác ABC.
O là giao điểm của DM và EN, ta có O là giao điểm hai đường chéo của hình thang DMEN.
...Xem thêm
bạn cũng fan Quang Hùng MasterD giống mình hả
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
16788
-
9683
-
Đã trả lời bởi chuyên gia
8082
-
7117
Thành viên hăng hái nhất trong tuần
-
✎ʏᴜᴜᰔᩚ
470 điểm
-
CHỈ YÊU MÌK EM | K12 ♡ ... ? 340 điểm
-
Minh nè:))
170 điểm
-
HỌC BÁ 8B5❤️🔥💯
165 điểm
-
$$\color{orange}{꧁ ঔ ৣ ☬ ✞ ⨳₳₪™ ⨳ ✞ ☬ ঔ ৣ ꧂}$$
105 điểm
-
Nguyễn Thị Quỳnh Mai
90 điểm
-
nam anh
85 điểm
-
My Ngoc 80 điểm
-
Minh Quan
70 điểm
-
hoàng chí vỹ 65 điểm
-
đka9A1
60 điểm
-
누가 고철을 팔고 싶어할까요?️?️
60 điểm
-
Đỗ Quyên
50 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
4 năm trước11955
-
4 năm trước11328
-
4 năm trước10003
-
4 năm trước10295
-
4 năm trước9729
Gửi báo cáo thành công!
