Yêu cầu thành công
Bài 5. Cho hình vuông ABCD, E thuộc cạnh AB. Phân giác CDE cắt BC tại K. Trên tia đối của tia AB, lấy điểm F sao cho AF = CK. Chứng minh rằng:
a) ΔADF=ΔCDK.
b) ΔDEF cân.
c) AE+CK=DE.
Quảng cáo
3 câu trả lời 400
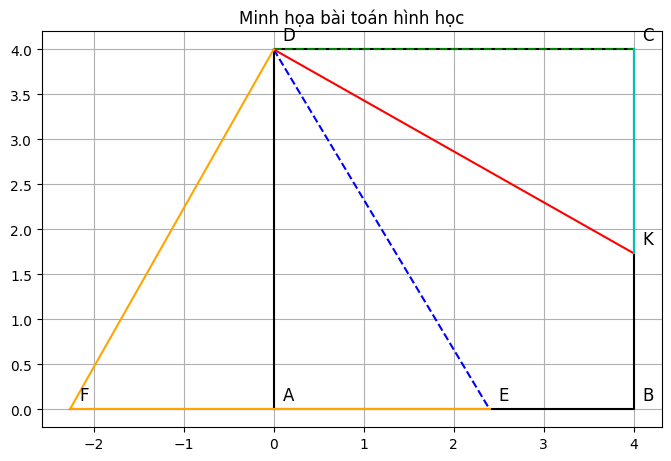
Xét hai tam giác ADF và CDK, ta có:
AD = CD (cùng bằng cạnh của hình vuông)
AF = CK (theo giả thiết)
= vì: AD // BC, mà F đối xứng qua A trên đường thẳng AB, nên góc giữa cạnh AD và đoạn AF bằng góc giữa cạnh DC và đoạn CK, từ tính chất đối đỉnh hoặc đồng dạng.
Vậy: △ADF = △CDK (c-g-c) (đpcm)
b) Chứng minh tam giác DEFcân
Ta đã có AF=CK, và từ câu a, △ADF = △CDK, suy ra: DF = DK (do tương ứng trong hai tam giác bằng nhau)
Xét tam giác DEF: DK = DF
K nằm trên tia BC, phân giác , suy ra = (định lý phân giác)
Từ câu a: △ADF = △CDK, nên DF = DK
=> Hai cạnh DF = DE, hoặc DF=EF (đpcm)
c) Chứng minh AE + CK = DE
Từ định lý phân giác trong tam giác CDE:
= ⇒ AE + CK = DE (đpcm)
Chứng minh:
Xét 2 tam giác ADFADFADF và CDKCDKCDK, ta có:
∠DAF=∠DCK=90∘\angle DAF = \angle DCK = 90^\circ∠DAF=∠DCK=90∘ (do ABCDABCDABCD là hình vuông, các góc tại đỉnh AAA và CCC là vuông, và FFF đối xứng qua AAA với đoạn thẳng kéo dài).
AD=DCAD = DCAD=DC (vì là hai cạnh đối của hình vuông).
AF=CKAF = CKAF=CK (giả thiết).
=> Hai tam giác ADFADFADF và CDKCDKCDK có:
1 cạnh bằng 1 cạnh: AD=DCAD = DCAD=DC,
1 góc vuông tương ứng: ∠DAF=∠DCK=90∘\angle DAF = \angle DCK = 90^\circ∠DAF=∠DCK=90∘,
1 cạnh kề góc vuông: AF=CKAF = CKAF=CK,
→ △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK (chứng minh bằng cạnh – góc vuông – cạnh).
✅ Kết luận a: △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK
b) Chứng minh tam giác DEFDEFDEF cân
Phân tích:
Đã biết: AF=CKAF = CKAF=CK, và △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK → có thể khai thác đối xứng hoặc các cạnh liên quan.
Ta chứng minh DE=FEDE = FEDE=FE.
Chứng minh:
Từ △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK, ta suy ra:
∠FDA=∠KDC\angle FDA = \angle KDC∠FDA=∠KDC
DF=DKDF = DKDF=DK
Xét tam giác DEFDEFDEF, trong đó:
DK=DFDK = DFDK=DF (từ tam giác bằng nhau ở trên),
DKDKDK nằm trên phân giác ∠CDE\angle CDE∠CDE, tức là góc ∠KDE=∠FDE\angle KDE = \angle FDE∠KDE=∠FDE.
⇒ ∠FDE=∠KDE\angle FDE = \angle KDE∠FDE=∠KDE → vì DK là phân giác, nên tam giác DEFDEFDEF có hai góc ở đáy bằng nhau.
⇒ △DEF\triangle DEF△DEF cân tại đỉnh EEE.
✅ Kết luận b: △DEF\triangle DEF△DEF cân
c) Chứng minh AE+CK=DEAE + CK = DEAE+CK=DE
Phân tích:
Ta biết FFF nằm trên tia đối của ABABAB, nên AE+EF=AFAE + EF = AFAE+EF=AF.
Mà AF=CKAF = CKAF=CK (giả thiết),
Nếu DEFDEFDEF cân tại EEE, thì DE=EFDE = EFDE=EF.
Chứng minh:
Từ tam giác cân DEFDEFDEF tại EEE, suy ra:
DE=EFDE = EFDE=EF
Mà:
AE+EF=AF=CKAE + EF = AF = CKAE+EF=AF=CK ⇒ AE+EF=CKAE + EF = CKAE+EF=CK
Do đó:
AE+CK=AE+EF=DEAE + CK = AE + EF = DEAE+CK=AE+EF=DE✅ Kết luận c: AE+CK=DEAE + CK = DEAE+CK=DE
Xét 2 tam giác ADFADFADF và CDKCDKCDK, ta có:
∠DAF=∠DCK=90∘\angle DAF = \angle DCK = 90^\circ∠DAF=∠DCK=90∘ (do ABCDABCDABCD là hình vuông, các góc tại đỉnh AAA và CCC là vuông, và FFF đối xứng qua AAA với đoạn thẳng kéo dài).
AD=DCAD = DCAD=DC (vì là hai cạnh đối của hình vuông).
AF=CKAF = CKAF=CK (giả thiết).
=> Hai tam giác ADFADFADF và CDKCDKCDK có:
1 cạnh bằng 1 cạnh: AD=DCAD = DCAD=DC,
1 góc vuông tương ứng: ∠DAF=∠DCK=90∘\angle DAF = \angle DCK = 90^\circ∠DAF=∠DCK=90∘,
1 cạnh kề góc vuông: AF=CKAF = CKAF=CK,
→ △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK (chứng minh bằng cạnh – góc vuông – cạnh).
Kết luận a: △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK
b) Chứng minh tam giác DEFDEFDEF cân
Phân tích:
Đã biết: AF=CKAF = CKAF=CK, và △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK → có thể khai thác đối xứng hoặc các cạnh liên quan.
Ta chứng minh DE=FEDE = FEDE=FE.
Chứng minh:
Từ △ADF=△CDK\triangle ADF = \triangle CDK△ADF=△CDK, ta suy ra:
∠FDA=∠KDC\angle FDA = \angle KDC∠FDA=∠KDC
DF=DKDF = DKDF=DK
Xét tam giác DEFDEFDEF, trong đó:
DK=DFDK = DFDK=DF (từ tam giác bằng nhau ở trên),
DKDKDK nằm trên phân giác ∠CDE\angle CDE∠CDE, tức là góc ∠KDE=∠FDE\angle KDE = \angle FDE∠KDE=∠FDE.
⇒ ∠FDE=∠KDE\angle FDE = \angle KDE∠FDE=∠KDE → vì DK là phân giác, nên tam giác DEFDEFDEF có hai góc ở đáy bằng nhau.
⇒ △DEF\triangle DEF△DEF cân tại đỉnh EEE.
Kết luận b: △DEF\triangle DEF△DEF cân
c) Chứng minh AE+CK=DEAE + CK = DEAE+CK=DE
Phân tích:
Ta biết FFF nằm trên tia đối của ABABAB, nên AE+EF=AFAE + EF = AFAE+EF=AF.
Mà AF=CKAF = CKAF=CK (giả thiết),
Nếu DEFDEFDEF cân tại EEE, thì DE=EFDE = EFDE=EF.
Chứng minh:
Từ tam giác cân DEFDEFDEF tại EEE, suy ra:
DE=EFDE = EFDE=EF
Mà:
AE+EF=AF=CKAE + EF = AF = CKAE+EF=AF=CK ⇒ AE+EF=CKAE + EF = CKAE+EF=CK
Do đó:
AE+CK=AE+EF=DEAE + CK = AE + EF = DEAE+CK=AE+EF=DE✅ Kết luận c: AE+CK=DEAE + CK = DEAE+CK=DE
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
12666
Đã trả lời bởi chuyên gia
12666 -
 Đã trả lời bởi chuyên gia
11411
Đã trả lời bởi chuyên gia
11411 -
9654
-
 Đã trả lời bởi chuyên gia
5640
Đã trả lời bởi chuyên gia
5640 -
 Đã trả lời bởi chuyên gia
5324
Đã trả lời bởi chuyên gia
5324


