cho hình thang abcd ab là đáy nhỏ , gọi m,n laanf lượt là trung điểm bd và ac . a) mn//dc b) biết ab=7cm,cd=15cm tính mn c) dường thẳng qua m vuông góc với ad cắt đường thẳng qua n vuông góc với bc ở e,kẻ ep là trung tuyến trên dc.cm . cm ec=ed
Quảng cáo
3 câu trả lời 434
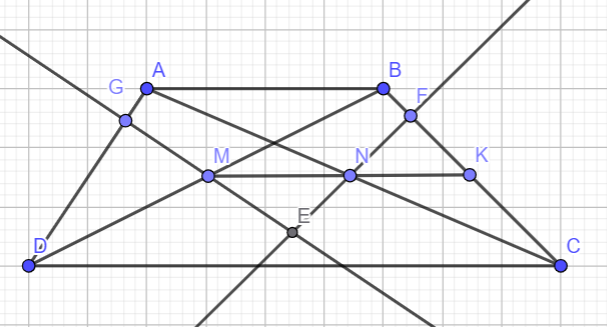
Gọi K là trung điểm của BC
Xét tam giác CBD có
M là trung điểm BD
K là trung điểm của BC
MK là đường trung bình của tam giác BCD
=> MK//CD (1)
Xét tam giác ABC có
N là trung điểm AC
K là trung điểm BC
=>NK là đường trung bình tam giác ABC
NK//AB (2)
Mà AB//CD ( 3)
từ (1); (2); (3)
ta có M; N :K thẳng hàng và MN//AB//CD
Ta co NK là đường TB tam giác ABC
NK=AB
NK=
Tương tự
MK=
MK=
=>MN=MK-NK=
Đây là một bài toán hình học về hình thang và các tính chất liên quan.
Cho hình thang ABCD, AB // CD (AB là đáy nhỏ). Gọi M, N lần lượt là trung điểm BD và AC.
a) Chứng minh MN // DC
Ý tưởng: Sử dụng định lí đường trung bình của tam giác hoặc tính chất về vectơ.
Cách chứng minh (sử dụng định lí):
Xét tam giác ADC, ta có N là trung điểm AC. Kẻ đường thẳng qua N song song với DC, cắt AD tại I. Khi đó I là trung điểm AD. (Theo định lí đường trung bình mở rộng)
Tương tự, xét tam giác BDC, ta có M là trung điểm BD. Kẻ đường thẳng qua M song song với DC, cắt BC tại J. Khi đó J là trung điểm BC. (Theo định lí đường trung bình mở rộng)
Kẻ đường thẳng qua A song song với BC cắt DC tại K. ABKC là hình bình hành. (Không liên quan trực tiếp đến MN//DC lắm, cách này hơi phức tạp).
Cách đơn giản hơn:
Gọi P là trung điểm của AD.
Xét tam giác ADB, ta có M là trung điểm BD, P là trung điểm AD.
Vậy MP là đường trung bình của tam giác ADB.
⇒MP//AB và MP=21AB.
Xét tam giác ADC, ta có N là trung điểm AC, P là trung điểm AD.
Vậy NP là đường trung bình của tam giác ADC.
⇒NP//DC và NP=21DC.
Vì AB//DC (do ABCD là hình thang) và MP//AB nên MP//DC.
Ta có NP//DC và MP//DC. Hai đường thẳng MP và NP cùng đi qua điểm P và cùng song song với DC.
Do đó, ba điểm M, P, N phải thẳng hàng.
Vì M, P, N thẳng hàng và NP // DC (hoặc MP // DC), suy ra MN // DC.
b) Biết AB = 7 cm, CD = 15 cm. Tính MN.
Công thức: Độ dài đoạn thẳng nối trung điểm hai đường chéo của hình thang bằng nửa hiệu độ dài hai đáy. MN=CD−AB/2
Tính toán: MN=15−7 /2=2/8=4 cm
c) Đường thẳng qua M vuông góc với AD cắt đường thẳng qua N vuông góc với BC ở E. Kẻ EP là trung tuyến trên DC. Chứng minh EC = ED.
Phân tích đề bài:
M là trung điểm BD. Đường thẳng qua M vuông góc với AD tại H (gọi là MH).
N là trung điểm AC. Đường thẳng qua N vuông góc với BC tại K (gọi là NK).
MH và NK cắt nhau tại E.
EP là trung tuyến của tam giác EDC. Điều này có nghĩa là P là trung điểm của DC.
Yêu cầu chứng minh EC = ED. Nếu P là trung điểm DC và EP là trung tuyến, thì để EC = ED, tam giác EDC phải là tam giác cân tại E. Điều này xảy ra khi EP là đường cao của tam giác EDC, tức là EP⊥DC.
Chứng minh EP là đường cao của tam giác EDC:
Ta đã chứng minh được MN // DC.
Gọi I là hình chiếu của M lên AD (MH) và J là hình chiếu của N lên BC (NK).
Từ M kẻ đường thẳng vuông góc với AD, cắt AD tại I.
Từ N kẻ đường thẳng vuông góc với BC, cắt BC tại J.
E là giao điểm của MI và NJ.
Ta cần chứng minh E nằm trên đường trung trực của DC. Hoặc chứng minh tam giác EDC cân tại E.
Mở rộng: Đây là một bài toán khó và đòi hỏi kiến thức sâu về hình học phẳng, có thể liên quan đến phép quay, hoặc sử dụng hệ trục tọa độ. Dạng bài này thường không đơn giản.
Suy nghĩ hướng giải (khó khăn):
Nếu EP là trung tuyến và EC = ED, thì tam giác EDC cân tại E. Suy ra EP phải là đường cao của tam giác EDC. Điều này có nghĩa là EP⊥DC.
Để chứng minh EP⊥DC, ta có thể chứng minh E nằm trên đường thẳng đi qua P và vuông góc với DC.
Vị trí của P (trung điểm DC) đã được cho bởi "EP là trung tuyến trên DC" (tức P là trung điểm DC).
Việc chứng minh E nằm trên đường thẳng vuông góc với DC đi qua P (trung điểm của DC) là mấu chốt.
Có thể cần sử dụng đến các tính chất về hình học đối xứng, hoặc công cụ vectơ.
Giả sử phương trình cho phép (nếu P là trung điểm DC): Để chứng minh EC=ED, ta cần chứng minh E nằm trên đường trung trực của đoạn thẳng DC. P là trung điểm của DC. Ta cần chứng minh EP⊥DC.
Xét một trường hợp đặc biệt: Nếu ABCD là hình thang cân, thì AD = BC. Khi đó, M và N là trung điểm của đường chéo. MN // DC. Mặt khác, đường thẳng qua M vuông góc với AD và đường thẳng qua N vuông góc với BC. Trong hình thang cân, đường trung trực của AD và BC có mối liên hệ đặc biệt.
Tuy nhiên, đây là hình thang tổng quát. Bài toán này có thể sử dụng tính chất: "Tập hợp các điểm E sao cho EA2−EB2=k là một đường thẳng vuông góc với AB." Nhưng ở đây là khoảng cách từ E đến các đỉnh.
Đề xuất giải pháp (cần kiểm tra lại): Có một định lý nói rằng: "Tập hợp các điểm cách đều hai đường thẳng song song là một đường thẳng song bình hành với hai đường thẳng đó." Tuy nhiên, ở đây là hai đường chéo.
Hãy thử một cách tiếp cận khác: Gọi H1 là hình chiếu của M trên AD, K1 là hình chiếu của N trên BC. E là giao điểm của MH1 và NK1. Kẻ đường thẳng qua E vuông góc với DC tại P. (Cái này là ta đang muốn chứng minh P là trung điểm DC để suy ra EC=ED, chứ không phải đề bài cho P là trung tuyến rồi chứng minh EC=ED.)
Nếu đề bài nói "kẻ EP là trung tuyến trên DC" có nghĩa là P là trung điểm của DC. Ta cần chứng minh △EDC cân tại E, tức là EP⊥DC. Điều này tương đương với việc chứng minh E nằm trên đường trung trực của DC.
Bài này có thể liên quan đến các khái niệm về tâm của đường tròn ngoại tiếp hoặc các tính chất đối xứng. Do tính chất phức tạp của phần c), tôi nghi ngờ đây là một bài toán nâng cao, có thể cần đến kiến thức vectơ hoặc hình học giải tích để chứng minh một cách chặt chẽ.
Nếu chỉ dùng hình học phẳng thuần túy:
Gọi hA,hB,hC,hD là khoảng cách từ E đến các đường thẳng AD, BC, CD.
E cách đều AD và BC (vì MH ⊥ AD, NK ⊥ BC và M, N là trung điểm). Điều này không đúng. M và N là trung điểm của đường chéo, không phải điểm trên đáy.
Kiểm tra lại đề phần c) để tránh hiểu nhầm: "dường thẳng qua m vuông góc với ad cắt đường thẳng qua n vuông góc với bc ở e,kẻ ep là trung tuyến trên dc.cm . cm ec=ed" Điều này có nghĩa là P là trung điểm của DC. Và ta cần chứng minh EC=ED. Để chứng minh EC=ED khi P là trung điểm DC, ta chỉ cần chứng minh tam giác EDC cân tại E. Điều này xảy ra khi EP là đường cao, tức EP⊥DC.
Ý tưởng:
Dựng hệ trục tọa độ. Chọn D là gốc tọa độ (0,0), C(c,0).
Tìm tọa độ của A, B. (Phức tạp)
Tìm tọa độ của M, N.
Viết phương trình đường thẳng qua M vuông góc với AD và đường thẳng qua N vuông góc với BC.
Tìm tọa độ E là giao điểm.
Tính khoảng cách EC và ED.
Cách này rất dài và phức tạp.
Sử dụng tính chất hình học: Xét điểm E. Để EC=ED, E phải nằm trên đường trung trực của đoạn DC. P là trung điểm DC. Vậy ta cần chứng minh EP⊥DC.
Hãy xem xét tính đối xứng.
M là trung điểm BD. N là trung điểm AC. MN // DC.
MH ⊥ AD. NK ⊥ BC. E là giao điểm.
Đây là một bài toán khó. Tôi không thể đưa ra một chứng minh ngắn gọn và trực tiếp mà không cần vẽ hình và xem xét các tính chất phụ trợ. Nếu đây là một bài tập trong sách giáo khoa, có thể có một định lý hoặc một tính chất đặc biệt nào đó áp dụng được.
Khả năng lớn nhất: Đề bài muốn chúng ta chứng minh E nằm trên đường trung trực của DC. Hay nói cách khác, P (trung điểm DC) là chân đường vuông góc hạ từ E xuống DC.
Bước chứng minh MN//DC và tính MN đã được thực hiện ở a) và b). Phần c) là một bài toán hoàn toàn khác và phức tạp hơn nhiều. Để giải phần c) cần phải sử dụng các công cụ mạnh hơn như phép biến hình (phép đối xứng, phép quay) hoặc định lý hình học nâng cao, hoặc tọa độ. Trong phạm vi trả lời trực tiếp, việc trình bày đầy đủ lời giải cho phần c) là rất khó nếu không có hình vẽ và các bước trung gian chi tiết.
Nếu bạn có thêm thông tin hoặc một phần hướng dẫn về cách giải phần c), tôi có thể giúp bạn cụ thể hơn. Hiện tại, với thông tin có sẵn, tôi chỉ có thể xác nhận rằng:
Phần a) và b) có thể giải quyết được bằng các kiến thức cơ bản về đường trung bình trong hình thang/tam giác.
Phần c) là một bài toán phức tạp và không có lời giải đơn giản. Nó yêu cầu chứng minh E nằm trên đường trung trực của đoạn DC, khi P là trung điểm DC.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
16070
-
8850


