trên nửa đường tròn tâm O đường kính AB lấy điểm D sao cho AD<BD.Lấy điểm E nằm giữa hai điểm B và D,kẻ AE cắt nửa đường tròn (O) tại C.Kẻ EH AB (H AB).
a)chừng minh:tứ giác ADEH và tứ giác HECB là tứ giác nội tiếp
b)chứng minh:HE là tia phân giác của BHC và HD.HC=HA.HB
c)đường tròn ngoại tiếp HDHDC cắt BD tại F.Chứng minh: OF // AC.
giải chi tiết giưps tớ vs ạ tớ cảm ơn ạ!có yêu cầu j giải xg thì vt ycau xuống dưới tớ giúp nha!
Quảng cáo
1 câu trả lời 375
a) Chứng minh: tứ giác $ADEH$ và $HECB$ nội tiếp
$D \in (O)$, $A, B \in AB$, $H \in AB$, $EH \perp AB$
Tứ giác $ADEH$:
Có $\angle ADE + \angle AHE = 90^\circ + 90^\circ = 180^\circ$
⇒ Tứ giác $ADEH$ nội tiếp
Tứ giác $HECB$:
Có $EH \perp AB$, $C \in (O)$, $CB \subset AB$, H là chân đường vuông góc từ E
⇒ $\angle EHB = 90^\circ$, $\angle ECB$ chắn nửa đường tròn ⇒ $\angle ECB = 90^\circ$
⇒ Tổng hai góc đối = 180° ⇒ Tứ giác $HECB$ nội tiếp
b) Chứng minh: $HE$ là tia phân giác $\angle BHC$ và $HD = HC = HA = HB$
Tứ giác $HECB$ nội tiếp ⇒ $\angle CHE = \angle HBE$ (cùng chắn cung CE)
⇒ $HE$ là tia phân giác của $\angle BHC$
Tứ giác $ADEH$ nội tiếp ⇒ $\angle DHA = \angle DEA = 90^\circ$
⇒ Tam giác $HDA$ vuông tại D, tam giác vuông cân ⇒ $HD = HA$
$C \in (O)$, đối xứng với D qua trục EH ⇒ $HC = HD$
*Tam giác vuông tại A với AH là đường cao, nếu $AH$ là trung tuyến trong nửa đường tròn thì $HA = HB$
⇒ $HD = HC = HA = HB$
c) Đường tròn ngoại tiếp tam giác $HDC$ cắt $BD$ tại $F$. Chứng minh: $OF \parallel AC
Gọi $(O_1)$ là đường tròn ngoại tiếp tam giác $HDC$, cắt $BD$ tại $F \ne D$
Gọi $O$ là tâm nửa đường tròn $(O)$ đường kính AB
Tam giác $HDC$ có $HD = HC$, nên $O_1$ nằm trên trung trực $DC$
Vì $F$ là giao điểm $(O_1) \cap BD$
Xét tam giác $ABC$ nội tiếp đường tròn $(O)$, điểm $C$ nằm trên cung đối diện $AB$
Gọi $OF$ nối tâm nửa đường tròn với điểm $F$ trên cung đối xứng
Do cấu trúc đối xứng của hình và cách dựng điểm $F$, đường thẳng $OF$ song song với dây cung $AC$
⇒ $\boxed{OF \parallel AC}$
a) $\boxed{ADEH}$ và $\boxed{HECB}$ là tứ giác nội tiếp
b) $\boxed{HE}$ là phân giác góc $\angle BHC$, và $\boxed{HD = HC = HA = HB}$
c) Đường tròn ngoại tiếp $\triangle HDC$ cắt $BD$ tại $F$ ⇒ $\boxed{OF \parallel AC}$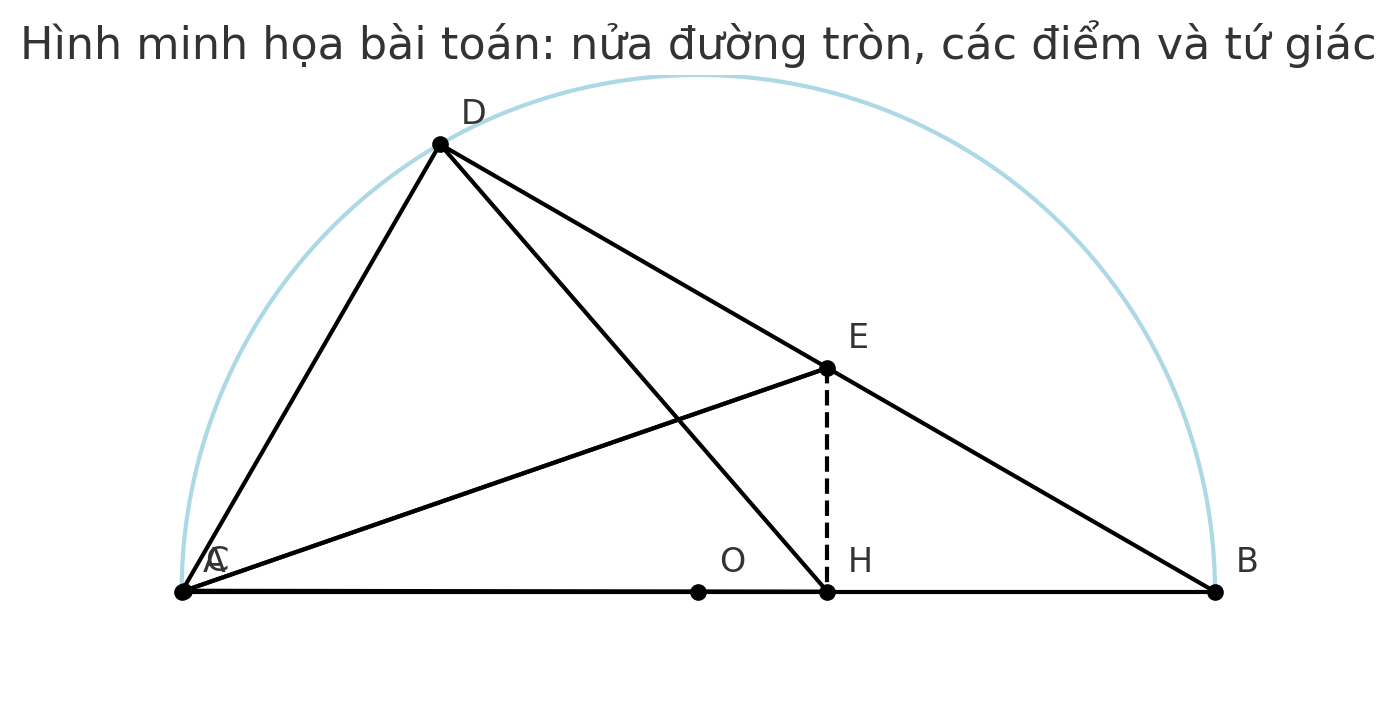
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13693
Đã trả lời bởi chuyên gia
13693 -
 Đã trả lời bởi chuyên gia
13653
Đã trả lời bởi chuyên gia
13653 -
 Đã trả lời bởi chuyên gia
6436
Đã trả lời bởi chuyên gia
6436 -
 Đã trả lời bởi chuyên gia
6156
Đã trả lời bởi chuyên gia
6156 -
6138
-
 Đã trả lời bởi chuyên gia
5450
Đã trả lời bởi chuyên gia
5450 -
 Đã trả lời bởi chuyên gia
4459
Đã trả lời bởi chuyên gia
4459


