Cho tam giác ABC có BM, CN là các đường trung tuyến ( BM < CN), G
là trọng tâm. Từ điểm D bất kỳ thuộc cạnh BC kẻ DE song song CN, DF song
song BM ( E thuộc AB, F thuộc AC). Gọi I, K là giao điểm của EF với BM, CN.
Chứng minh rằng EI = IK = KF
Quảng cáo
1 câu trả lời 302
Bài làm:
Từ giả thiết:
DE // CN ⇒ ΔDBE ∼ ΔNCG (vì DE // CN, theo định lý Ta-lét)
DF // BM ⇒ ΔDCF ∼ ΔMBG
Ta xét hình bình hành DEFC được tạo bởi hai đường song song với hai đường trung tuyến CN và BM. Do đó, EF song song với MN (MN là đoạn nối trung điểm của AB và AC), và EF cắt hai đường BM và CN tại I và K.
Ta biết: G là trọng tâm tam giác ABC ⇒ G là giao điểm của 3 đường trung tuyến, và mỗi trọng tâm chia đường trung tuyến theo tỉ lệ:
BG GM = 2 : 1, CG : GN =2 :1
Xét tam giác BMN với EF cắt BM tại I, cắt CN tại K và EF // MN ⇒ theo định lý Ta-lét đảo, ta có:
⇒ EI = IK = KF
$\boxed{\text{EI = IK = KF}}$ 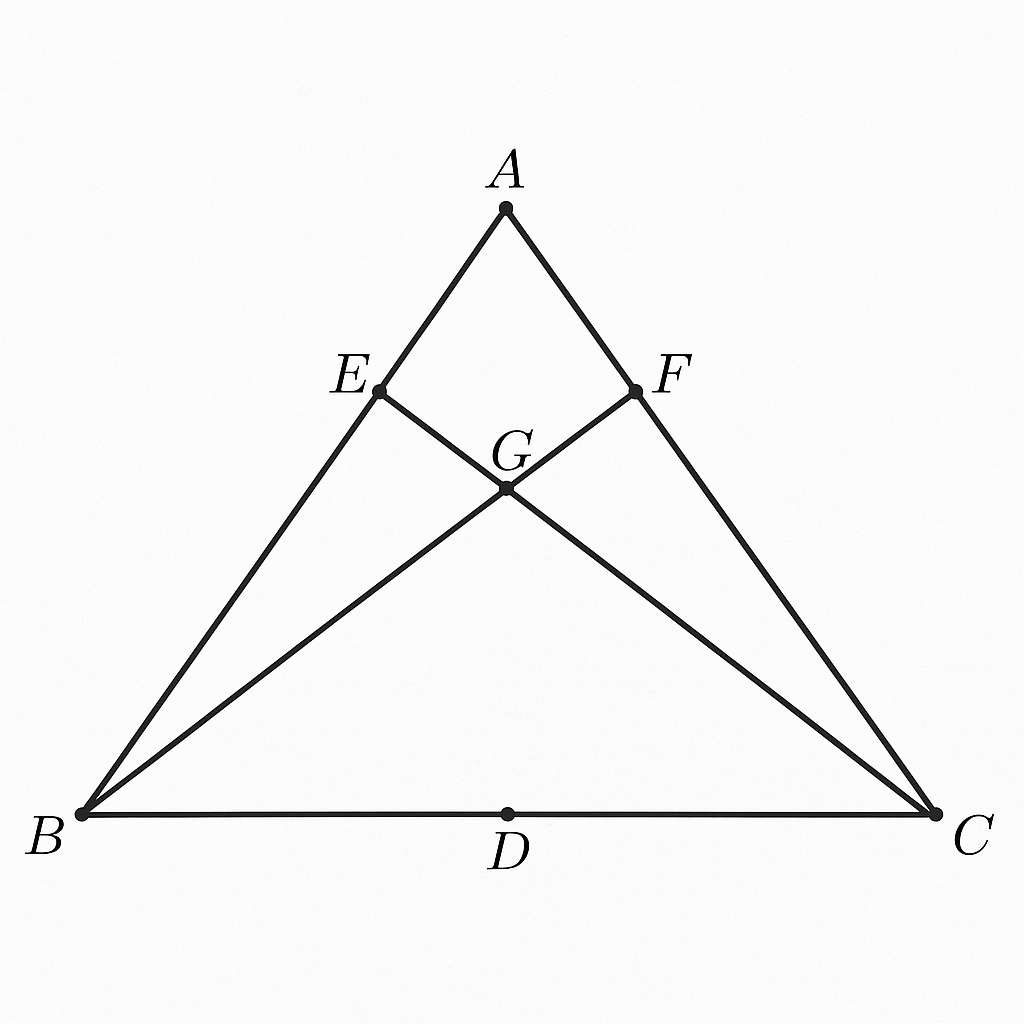
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13107
Đã trả lời bởi chuyên gia
13107 -
 Đã trả lời bởi chuyên gia
12034
Đã trả lời bởi chuyên gia
12034 -
 Đã trả lời bởi chuyên gia
8837
Đã trả lời bởi chuyên gia
8837 -
 Đã trả lời bởi chuyên gia
6708
Đã trả lời bởi chuyên gia
6708 -
6006


