Câu 2.
Cho ∆ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy điểm E sao cho AE = AB. Kẻ EI vuông góc với AH tại I, tia phân giác của BAC cắt BE tại M.
1) Chứng minh: ∆ABM vuông cân.
2) Chứng minh: AH = EI.
3) Chứng minh: AHM = 45°.
Quảng cáo
1 câu trả lời 480
1) Chứng minh tam giác ABM vuông cân
Ta có:
∆ABC vuông tại A ⇒ ∠BAC = 90°
AE = AB (giả thiết)
⇒ Xét tam giác ABE có AE = AB, mà ∠BAE là một phần của ∠CAB = 90°
⇒ ∠ABE = ∠AEB (tam giác cân tại A)
Gọi M là giao điểm của phân giác ∠BAC và đoạn BE. Vì AE = AB ⇒ tam giác ABE cân tại A ⇒ phân giác ∠BAC đồng thời là đường trung tuyến ứng với đáy BE
⇒ M là trung điểm của BE
Mà ∠A = 90°, M là trung điểm cạnh đối ⇒ tam giác ABM vuông cân tại A
⇒ ∆ABM vuông cân tại A.
2) Chứng minh AH = EI
Ta có:
∆ABC vuông tại A, AH là đường cao từ A ⇒ AH ⊥ BC
Kẻ EI ⊥ AH tại I ⇒ EI ⊥ AH
Xét tam giác vuông AHC và tam giác EIH, có:
∠EIH = ∠AHC = 90°
AE = AB (giả thiết), mà AB = AH (vì ∆ABM vuông cân ⇒ AB = AH)
⇒ AE = AH
Lại có: ∠AEI = ∠HAH = cùng bằng 90° ⇒ ∆AEI và ∆AHC bằng nhau
⇒ EI = AH
3) Chứng minh ∠AHM = 45°
Ta đã chứng minh:
∆ABM vuông cân tại A ⇒ ∠BAM = 45°
AH là đường cao, M nằm trên phân giác ∠BAC ⇒ ∠HAM = 45°
⇒ ∠AHM = 45°
1. ∆ABM vuông cân tại A
2. AH = EI
3. ∠AHM = 45°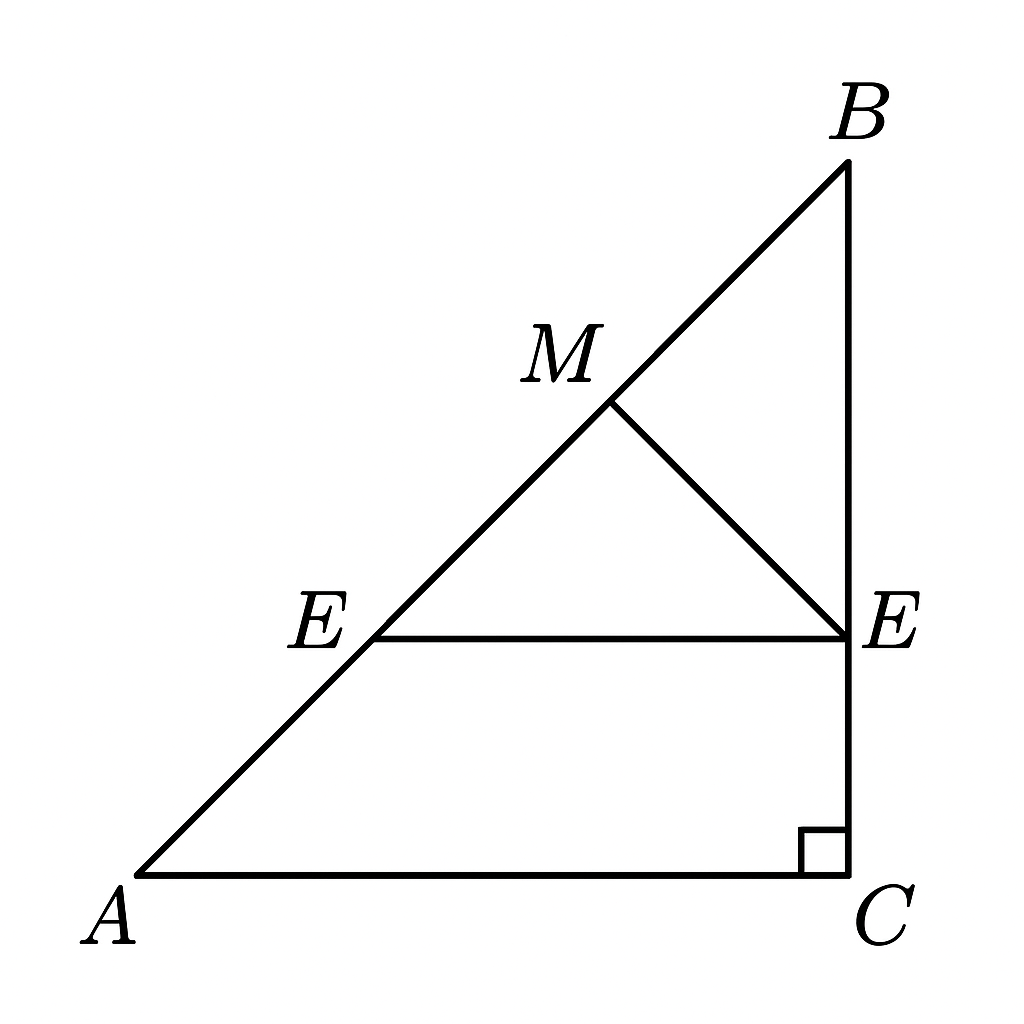 
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
4144
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4935
