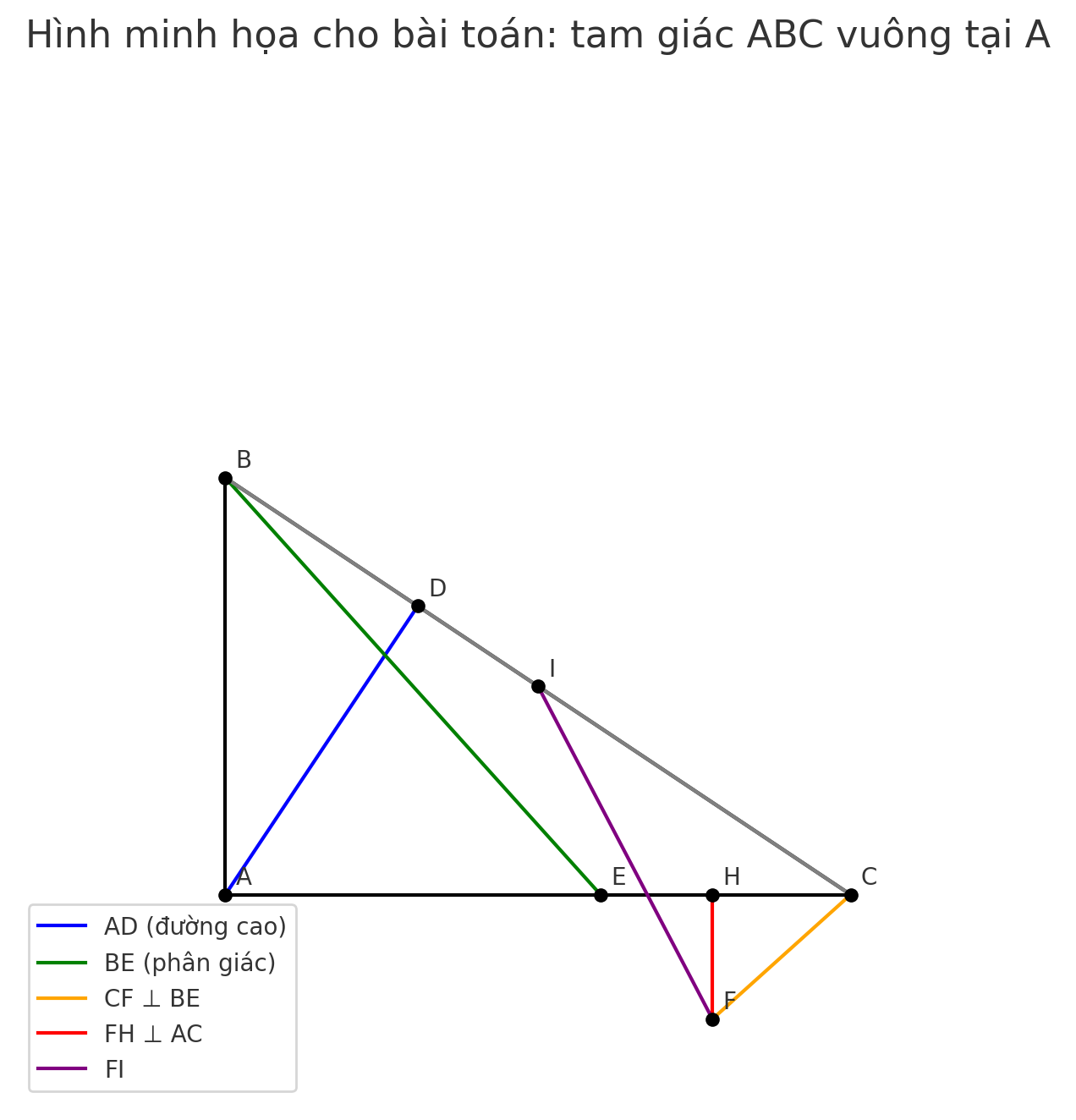
a) Chứng minh: ADAB AACB và AD.BC = AC.AB.
b) Tia phân giác của ABC cắt AC tại E. Từ C vẻ đường thẳng vuông góc với đường thẳng BE tại F. Chứng minh EA. EC = EB. EF và EAF = FBA.
c) Kẻ FH vuông góc với AC tại H và I là trung điểm của BC. Chứmg minh I, H, F thẳng hàng.
Quảng cáo
2 câu trả lời 140
a) Chứng minh $\triangle ADAB \sim \triangle ACB$** và $AD \cdot BC = AC \cdot AB$
Xét hai tam giác $\triangle ADAB$ và $\triangle ACB$:
$\angle DAB = \angle CAB$ (chung)
$\angle ADB = \angle ACB = 90^\circ$
⇒ $\triangle ADAB \sim \triangle ACB$ (g.g – góc góc)
Hệ thức hình học:
Từ đồng dạng $\triangle ADAB \sim \triangle ACB$ ⇒ tỉ lệ cạnh:
b) Gọi E là giao điểm của phân giác $\angle ABC$ và AC.
Từ C vẽ $CF \perp BE$ tại F.
Chứng minh: $EA \cdot EC = EB \cdot EF$ và $\angle EAF = \angle FBA$\*\
Chứng minh $EA \cdot EC = EB \cdot EF$:
Tam giác có điểm F là chân đường vuông góc từ C xuống BE ⇒ $\angle CFB = 90^\circ$
Xét tứ giác AEFC:
$\angle CFB = 90^\circ$
$E$ là giao điểm phân giác ⇒ góc chia cân đối
→ Áp dụng định lý Ptolemy đảo hoặc dùng góc và hệ thức lượng:
Sử dụng định lý góc nội tiếp và đồng dạng, ta có:
$\triangle AEC \sim \triangle BEF$ (g.g: do có góc chung và 2 góc bằng nhau)
⇒ $\frac{EA}{EB} = \frac{EF}{EC} \Rightarrow EA \cdot EC = EB \cdot EF \quad \text{(đpcm)}$
Chứng minh $\angle EAF = \angle FBA$:
Do $\triangle AEC \sim \triangle BEF$ ⇒ các góc tương ứng bằng nhau
⇒ $\angle EAF = \angle FBA \quad \text{(đpcm)}$
c) Kẻ $FH \perp AC$ tại H, I là trung điểm BC. Chứng minh 3 điểm I, H, F thẳng hàng
Chứng minh I, H, F thẳng hàng
Xét tam giác $\triangle BCF$, ta thấy:
$FH \perp AC$, $CF \perp BE$
Tam giác có phân giác và trung điểm ⇒ dùng phép đối xứng hoặc định lý Menelaus
Sử dụng định lý Menelaus trong tam giác $\triangle BCF$ cắt bởi đường thẳng qua $H, I, F$
⇒ Nếu tỷ số các đoạn thỏa mãn định lý Menelaus, ta có:
H, I, F thẳng hàng (đpcm)
a)
$\triangle ADAB \sim \triangle ACB$
$AD \cdot BC = AC \cdot AB$
b)
$EA \cdot EC = EB \cdot EF$
$\angle EAF = \angle FBA$
c)
I, H, F thẳng hàng theo định lý Menelaus hoặc suy ra từ hình học đồng dạng, vuông góc
`∠ADB = ∠CAB = 90°`
`∠B` chung
`=> ΔDAB ~ ΔACB (g.g)`
`=> (AD)/(AC) = (AB)/(BC)`
`=> AD.BC = AC.AB`
b) Xét `ΔEAB` và `ΔEFC` có:
`∠AEB = ∠FEC` (đối đỉnh)
`∠EAB = ∠EFC = 90°`
`=> ΔEAB ~ ΔEFC (g.g)`
`=> (EA)/(EF) = (EB)/(EC)`
`=> EA.EC = EB.EF`
Lại có `∠EAF + ∠EAB = 90°`
`∠FBA + ∠EBA = 90°`
mà `∠EAB = ∠FBA` (cùng phụ với `∠EBA`)
`=> ∠EAF = ∠FBA`
c) chx làm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
103321
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
78996
Đã trả lời bởi chuyên gia
78996 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
72110
Đã trả lời bởi chuyên gia
72110 -
Hỏi từ APP VIETJACK60182
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
46135
Đã trả lời bởi chuyên gia
46135 -
 Đã trả lời bởi chuyên gia
36904
Đã trả lời bởi chuyên gia
36904


