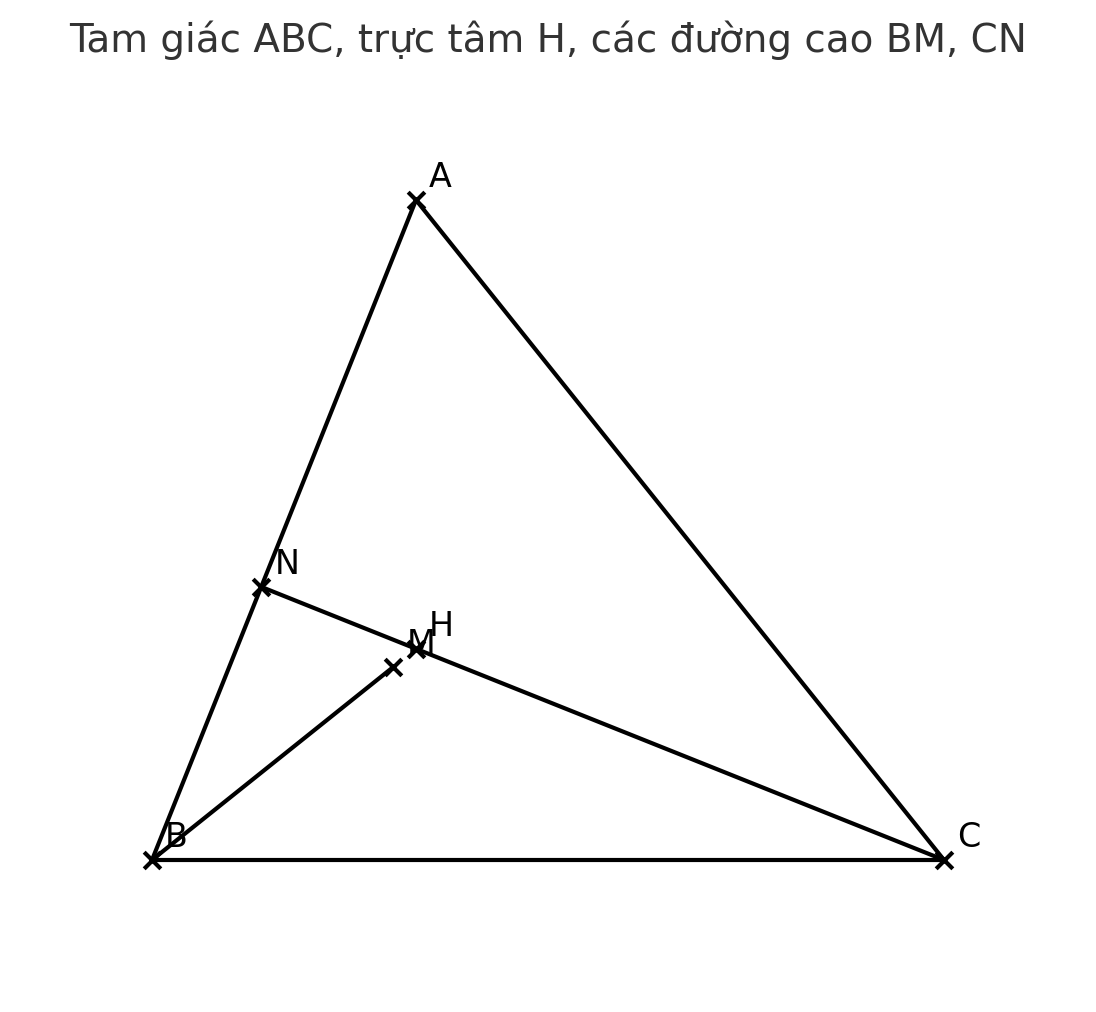
a) Chứng minh \(\triangle AMB \sim \triangle ANC\):

- Vì \(BM\) và \(CN\) là hai đường cao nên:
\[
BM \perp AC \quad \text{và} \quad CN \perp AB
\]
- Xét hai tam giác \(AMB\) và \(ANC\), ta có:
- \(\widehat{AMB} = 90^\circ\),
- \(\widehat{ANC} = 90^\circ\),
- \(\widehat{BAM} = \widehat{CAN}\) (vì cùng bằng góc tại đỉnh \(A\)).

→ Suy ra \(\triangle AMB \sim \triangle ANC\) (c.g.c: cạnh - góc vuông - cạnh).

Kết luận:
\[
{\triangle AMB \sim \triangle ANC}
\]

b) Chứng minh \(AB \times AN = AM \times AC\):

- Vì \(\triangle AMB \sim \triangle ANC\) nên các cặp cạnh tương ứng tỉ lệ:

\[
\frac{AM}{AN} = \frac{AB}{AC}
\]

- Nhân chéo ta được:

\[
AB \times AN = AM \times AC
\]

Kết luận:
\[
{AB \times AN = AM \times AC}
\]

c) Chứng minh \(BH \times BM + CH \times CN\) không đổi:
Trong tam giác vuông tại \(M\), có:
\[
BM^2 = BH \times BC
\quad \text{và tương tự} \quad CN^2 = CH \times BC
\]
Trong tam giác \(ABC\):

\[
S_{ABC} = \frac{1}{2} BC \times AH = \frac{1}{2} AB \times CN = \frac{1}{2} AC \times BM
\]

=>
\[
AB \times CN = AC \times BM
\]
(theo hệ thức lượng trong tam giác nhọn).

Mặt khác, theo hệ thức lượng đường cao:

\[
BH \times BM = CH \times CN
\]
khi \(A\) di chuyển trên cung tròn đường tròn cố định dựng trên \(BC\).

→ Vậy tổng \(BH.BM + CH.CN\) tỉ lệ với \(BC^2\), mà \(BC\) cố định.

→ Kết luận:
\[
{BH \times BM + CH \times CN \text{ có giá trị không đổi}}
\]