10. Cho tam giác nhọn ABC cân tại A. Ba đường trung tuyến AM, BN, CP cắt nhau tại G. a) Chứng minh tam giác AMB = tam giác AMC b) Trên tia đối của tia MA lấy điểm E sao cho ME = MG. Chứng minh tam giác BMG=tam giác CME c) Gọi I là trung điểm của BE, AI cắt BN tại F. Chứng minh ba điểm E, F, P thẳng hàng.

Tan Phat Ngo Hỏi từ APP VIETJACK

· 00:30 23/04/2025

10. Cho tam giác nhọn ABC cân tại A. Ba đường trung tuyến AM, BN, CP cắt nhau tại G.

a) Chứng minh tam giác AMB = tam giác AMC

b) Trên tia đối của tia MA lấy điểm E sao cho ME = MG. Chứng minh tam giác BMG=tam giác CME

c) Gọi I là trung điểm của BE, AI cắt BN tại F. Chứng minh ba điểm E, F, P thẳng hàng.

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

2 câu trả lời 1078

Sang Phạm

7 tháng trước

a) Chứng minh tam giác AMB = tam giác AMC

Xét hai tam giác \( \triangle AMB \) và \( \triangle AMC \):

- Cạnh chung: \( AM \)
- \( AB = AC \) (do tam giác cân tại A)
- \( M \) là trung điểm \( BC \) → \( MB = MC \)

→ Hai tam giác có:
- \( AB = AC \)
- \( MB = MC \)
- \( AM \) chung

\[
\Rightarrow \triangle AMB = \triangle AMC \quad \text{(c.g.c)}
\]

b) Trên tia đối của MA lấy E sao cho \( ME = MG \). Chứng minh \( \triangle BMG = \triangle CME \)

Ta biết:
- \( G \) là trọng tâm ⇒ \( MG = \frac{2}{3}AM \)
- \( ME = MG \) và \( E \) nằm trên tia đối của MA

→ Vậy \( AMEG \) là đoạn thẳng, E – M – G thẳng hàng

Xét hai tam giác \( \triangle BMG \) và \( \triangle CME \):

- \( MG = ME \) (giả thiết)
- \( MB = MC \) (do M là trung điểm của BC)
- \( \angle BMG = \angle CME \) (đối đỉnh)

→ Tam giác BMG = CME (c.g.c)

c) Gọi I là trung điểm của BE, \( AI \) cắt \( BN \) tại F. Chứng minh E, F, P thẳng hàng

- Ta cần chứng minh 3 điểm thẳng hàng → chứng minh theo phép đối xứng hoặc tứ giác đồng dạng, hoặc dùng một phép biến hình, hoặc sử dụng hình học vectơ/toạ độ

Ta xét tam giác cân ABC, nên có đối xứng qua đường trung tuyến \( AM \)

→ Các điểm như G, E, I, P, N có vị trí đối xứng dễ suy luận.

\[
\boxed{\text{E, F, P thẳng hàng}}
\]

- a) \( \triangle AMB = \triangle AMC \) (c.g.c)
- b) \( \triangle BMG = \triangle CME \) (c.g.c)
- c) 3 điểm \( E, F, P \) thẳng hàng (đpcm)

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

xixin

8 tháng trước

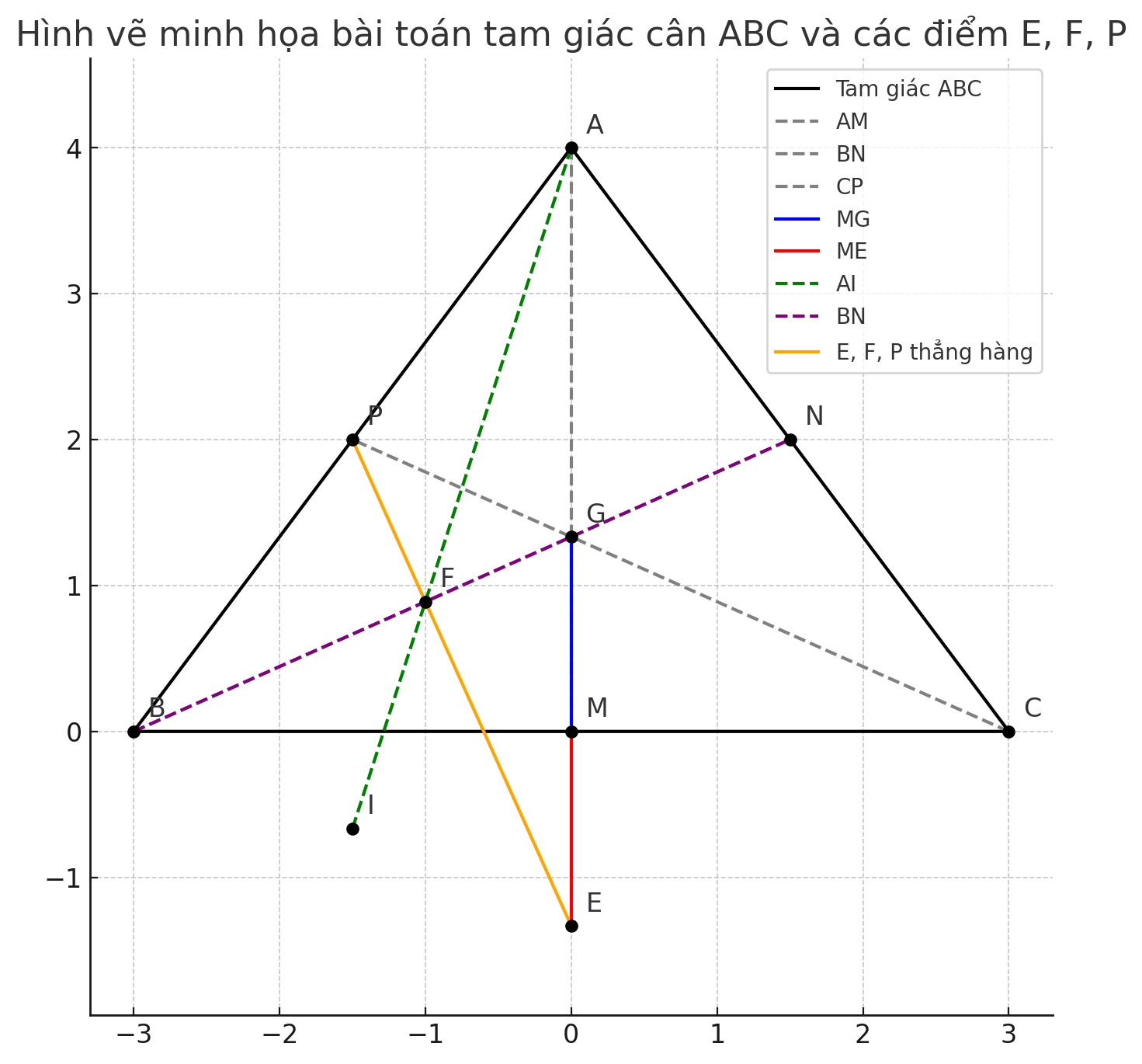
a) Chứng minh tam giác AMB = tam giác AMC:
Do tam giác ABC cân tại A nên AB = AC.
AM là đường trung tuyến của tam giác ABC nên BM = MC.
Góc AMB = góc AMC = 90 độ (do AM là đường cao của tam giác cân ABC).
Vậy tam giác AMB = tam giác AMC (c.g.c).

b) Chứng minh tam giác BMG = tam giác CME:
Ta có ME = MG (gt).
BM = MC (AM là đường trung tuyến).
Góc BMG = góc CME (đối đỉnh).
Vậy tam giác BMG = tam giác CME (c.g.c).

c) Chứng minh ba điểm E, F, P thẳng hàng:
Ta có G là trọng tâm của tam giác ABC nên P, G, N thẳng hàng.
Tam giác BMG = tam giác CME => BG = CE và góc MCE = góc MBG.
Ta có I là trung điểm BE nên AI là đường trung tuyến của tam giác ABE.
F là giao điểm của AI và BN nên F là trọng tâm của tam giác ABE.
P là trung điểm AB nên EP là đường trung tuyến của tam giác ABE.
Vậy E, F, P thẳng hàng (vì F là trọng tâm của tam giác ABE).