cho đường tròn tâm o, bán kính R và điểm C nằm ngoài đường tròn. Qua C kẻ đường thẳng d vuông góc với OC. Lấy điểm N bất kỳ trên d. Kẻ tiếp tuyến NA của O, A là tiếp điểm. 1. Chứng minh tứ giác ANCO là tứ giác nội tiếp. 2. Kẻ dây AB vuông góc với NO tại K, dây AB cắt OC tại M. , Chứng minh rằng NB là tiếp tuyến của (O) và tính OM. OC theo R. Kẻ đường kính AD của (O). vẽ BH vuông góc với AD tại H. Chứng minh ND đi qua trung điểm của BH.
Quảng cáo
1 câu trả lời 1077
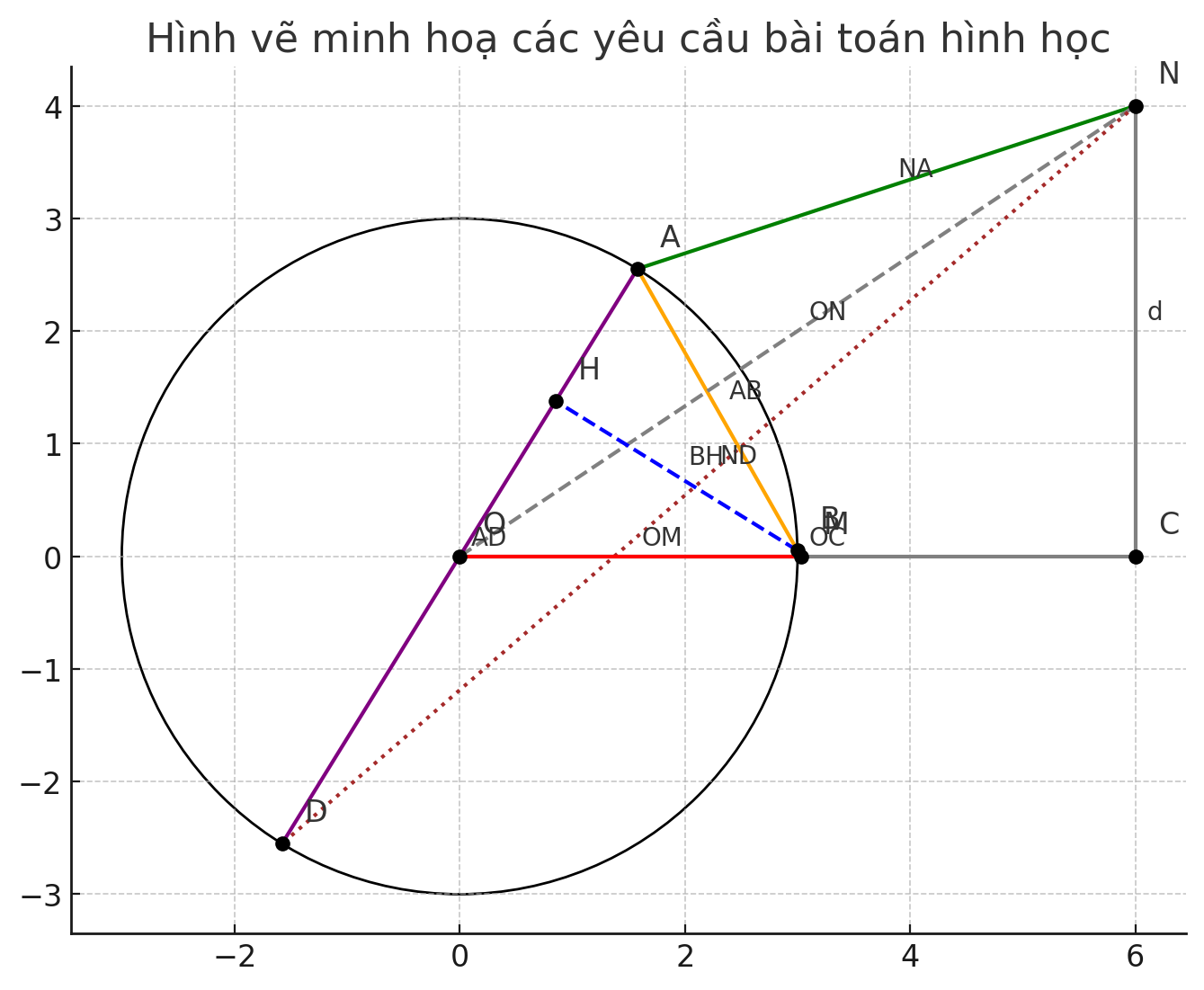
Tứ giác ANCO là tứ giác nội tiếp: Do góc giữa tiếp tuyến NA và bán kính OA là 90°, ⇒ góc ANC + góc AOC = 180° ⇒ nội tiếp.
Dây AB ⊥ NO tại K, cắt OC tại M
NB là tiếp tuyến với (O): vì góc giữa NB và OB là 90°
OM có thể tính được theo R bằng cách áp dụng tam giác vuông AOB hoặc định lý Pitago trong tam giác vuông OMB
AD là đường kính, BH ⊥ AD tại H ⇒ ND đi qua trung điểm BH (ứng với tính chất hình học đường tròn).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13693
Đã trả lời bởi chuyên gia
13693 -
 Đã trả lời bởi chuyên gia
13653
Đã trả lời bởi chuyên gia
13653 -
 Đã trả lời bởi chuyên gia
6436
Đã trả lời bởi chuyên gia
6436 -
 Đã trả lời bởi chuyên gia
6156
Đã trả lời bởi chuyên gia
6156 -
6138
-
 Đã trả lời bởi chuyên gia
5450
Đã trả lời bởi chuyên gia
5450 -
 Đã trả lời bởi chuyên gia
4459
Đã trả lời bởi chuyên gia
4459


