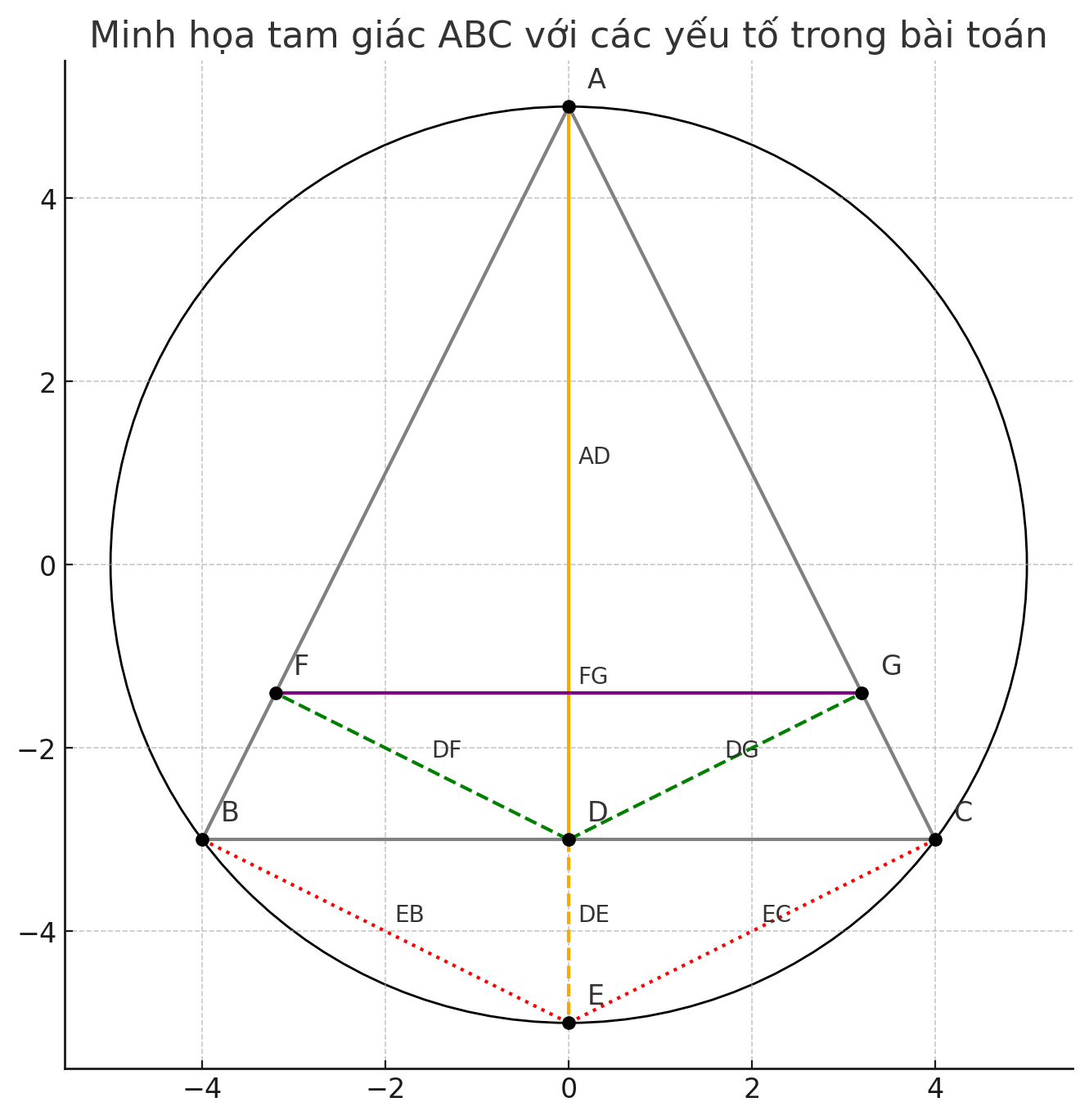
Cho tam giác ABC nội tiếp đường tròn (0), vẽ đường cao AD của tam giác ABC ; kéo
dài AD cắt đường tròn (O) ở E(E khác A) . Vẽ DF vuông góc với AB tại F, DG vuông góc với AC tại G. Chứng minh:
a) Tứ giác AFDG nội tiếp;
b) DA.DE = DB.DC
c)tam giác DFG ~ tam giác EBC
Quảng cáo
1 câu trả lời 290
a) Chứng minh tứ giác AFDG nội tiếp
Chứng minh:
Trong tứ giác AFDG, ta có:
- \( \angle AFD = 90^\circ \) (do \( DF \perp AB \))
- \( \angle AGD = 90^\circ \) (do \( DG \perp AC \))
⇒ Hai góc đối của tứ giác cùng bằng \(90^\circ\) ⇒ tứ giác AFDG nội tiếp đường tròn đường kính AD.
Tứ giác AFDG nội tiếp
b) Chứng minh: \( DA \cdot DE = DB \cdot DC \)
Nhận xét:
- A, B, C, E đều nằm trên đường tròn
- D nằm trên đường cao AD, cắt đường tròn tại E
⇒ Áp dụng định lý về hai dây cắt nhau (hoặc hệ thức đoạn thẳng):
- D nằm trên đường cao ⇒ đường thẳng qua D cắt đường tròn tại A và E ⇒ theo định lý tích đoạn thẳng:
\[
DA \cdot DE = DB \cdot DC
\]
Kết luận b: \( DA \cdot DE = DB \cdot DC \)
c) Chứng minh tam giác \( DFG \sim \triangle EBC \)
Chứng minh:
- Xét tam giác \(DFG\) và \(EBC\):
\( \angle DFG = \angle EBC \) vì:
- \(DF \perp AB\), mà \(AB\) là tiếp tuyến với góc EBC tại B
- Tương tự, \(DG \perp AC\), nên \( \angle DGF = \angle ECB \)
Các góc tương ứng bằng nhau ⇒ tam giác DFG đồng dạng với tam giác EBC theo g.g.g
Kết luận c \( \triangle DFG \sim \triangle EBC \)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13107
Đã trả lời bởi chuyên gia
13107 -
 Đã trả lời bởi chuyên gia
12034
Đã trả lời bởi chuyên gia
12034 -
 Đã trả lời bởi chuyên gia
8837
Đã trả lời bởi chuyên gia
8837 -
 Đã trả lời bởi chuyên gia
6708
Đã trả lời bởi chuyên gia
6708 -
6006


