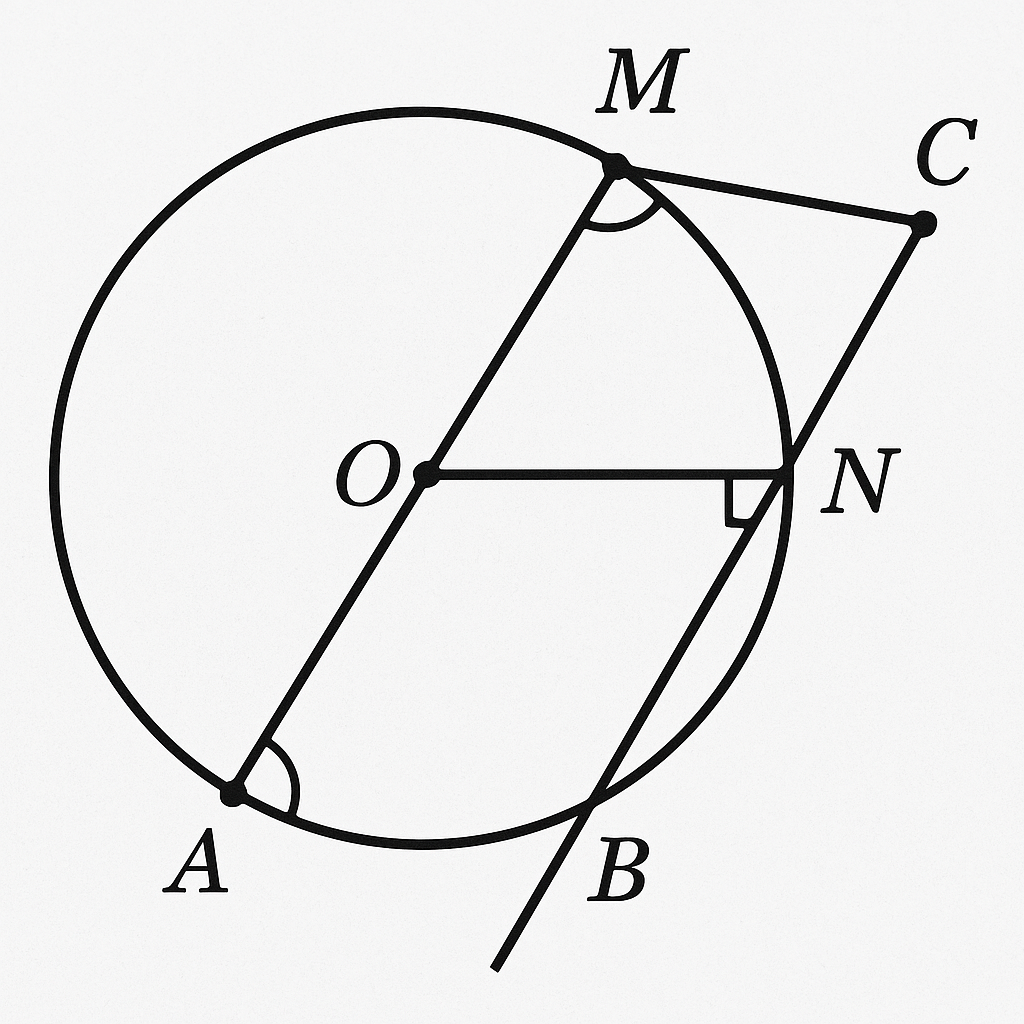
cho đường tròn (o) đường kính AB, tâm O và điểm M là một điểm trên đường tròn ( M khác A,B, MAMB ). tiếp tuyến của đường tròn ( o ) tại A cắt đường thẳng BM tại C. đường kính vuông góc với AB cắt MC tại N
a, chứng minh rằng tứ giác AMNO là tứ giác nội tiếp ( đã làm )
b, chứng minh góc OMB = góc CAM và MA^2= MB . MC
Quảng cáo
1 câu trả lời 626
a) Chứng minh tứ giác \( AMNO \) là tứ giác nội tiếp
Vì:
- \( AB \) là đường kính ⇒ \( \angle AMB = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
- Đường kính vuông góc với AB cắt MC tại N ⇒ \( ON \perp AB \) (vì là đường kính vuông góc với AB).
Ta xét tứ giác \( AMNO \):
- Trong tam giác \( AMB \), \( \angle AMB = 90^\circ \)
- \( O \) là trung điểm \( AB \), do \( AB \) là đường kính.
- \( ON \perp AB \), nên điểm \( N \) thuộc đường kính vuông góc với AB ⇒ \( ON \perp AB \)
=> \( \angle AMO + \angle ANO = 180^\circ \)
⇒ Tứ giác \( AMNO \) có tổng hai góc đối bằng \( 180^\circ \) ⇒ là tứ giác nội tiếp.
b) Chứng minh \( \angle OMB = \angle CAM \) và \( MA^2 = MB \cdot MC \)
1. Chứng minh \( \angle OMB = \angle CAM \)
- Xét tam giác \( OMB \) và góc \( OMB \) nằm trong đường tròn.
- Tia tiếp tuyến tại A ⇒ \( \angle CAM \) là góc tạo bởi tiếp tuyến và dây MA.
- Theo định lý: **Góc giữa tiếp tuyến và dây bằng góc nội tiếp chắn cùng cung, nên:
\[
\angle CAM = \angle OMB
\]
(vì cùng chắn cung \( MB \)).
2. Chứng minh \( MA^2 = MB \cdot MC \)
- Áp dụng định lý tiếp tuyến - cát tuyến:
Nếu từ điểm \( C \) ngoài đường tròn, kẻ tiếp tuyến \( CA \) và cát tuyến \( CBM \), thì:
\[
CA^2 = CB \cdot CM
\]
- Mà \( CA = MA \) (vì cùng đoạn từ M tới A)
⇒ \( MA^2 = MB \cdot MC \)
- a) Tứ giác \( AMNO \) nội tiếp
- b) \( \angle OMB = \angle CAM \), và \( MA^2 = MB \cdot MC \)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
13676
Đã trả lời bởi chuyên gia
13676 -
 Đã trả lời bởi chuyên gia
13621
Đã trả lời bởi chuyên gia
13621 -
 Đã trả lời bởi chuyên gia
6429
Đã trả lời bởi chuyên gia
6429 -
 Đã trả lời bởi chuyên gia
6148
Đã trả lời bởi chuyên gia
6148 -
6111
-
 Đã trả lời bởi chuyên gia
5440
Đã trả lời bởi chuyên gia
5440 -
 Đã trả lời bởi chuyên gia
4451
Đã trả lời bởi chuyên gia
4451


