Vì $AB = AC$, và $D \in AB$, nên ta xét tam giác cân tại A để khai thác đối xứng.

Ta có:

- $CE = BD$
- $M$ là trung điểm của $DE$

→ Nếu ta chứng minh $CB$ là đường trung trực của đoạn thẳng $DE$
thì điểm trung điểm $M$ của $DE$ sẽ nằm trên $CB$ ⇒ $B, C, M$ thẳng hàng.

Chứng minh: $CB$ là đường trung trực của $DE$

Xét 2 tam giác:

- Tam giác $ABD$
- Tam giác $ACE$

Vì:
- $AB = AC$ (tam giác cân)
- $BD = CE$ (gt)
- $\angle ABD = \angle ACE$ (đối đỉnh)

⇒ $\triangle ABD = \triangle ACE$ (c.g.c)

→ Suy ra:
$\angle CBD = \angle BCE$

→ Vậy tam giác $CDB$ cân tại $C$, và đường thẳng $CB$ chia $DE$ thành hai đoạn bằng nhau tại trung điểm $M$ ⇒ $CB \perp DE$ tại $M$

⇒ $CB$ là đường trung trực của $DE$
⇒ $M \in CB$

Suy ra $C, B, M$ thẳng hàng. Đpcm.

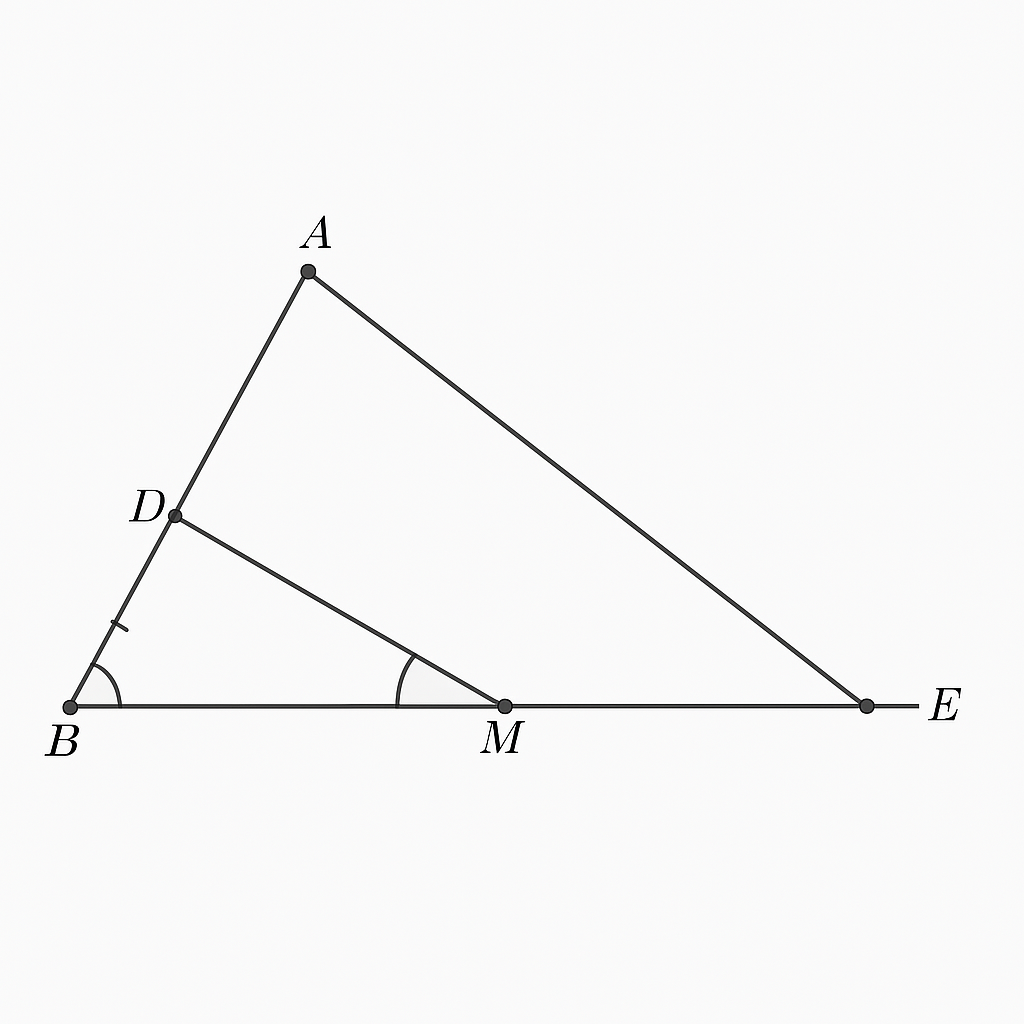
Để chứng minh ba điểm B, C, M thẳng hàng, ta cần chứng minh $\angle BCM + \angle MCA = 180^\circ$ hoặc $\angle BCM = \angle ACE$ (vì $C, A, E$ thẳng hàng).

**Phân tích:**

* Tam giác ABC cân tại A, nên $AB = AC$ và $\angle ABC = \angle ACB$.
* $CE = BD$ (giả thiết).
* M là trung điểm của DE, nên $DM = ME$.

**Chứng minh:**

1. **Gọi I là trung điểm của BE.**
* Xét tam giác BDE, ta có I là trung điểm BE, M là trung điểm DE.
* Suy ra IM là đường trung bình của tam giác BDE.
* Do đó, $IM // BD$ và $IM = \frac{1}{2}BD$.

2. **Chứng minh $IM // AC$**
* Vì $IM // BD$, mà $BD$ nằm trên $AB$, nên $IM // AB$.

3. **Chứng minh $IM = \frac{1}{2}CE$**
* Vì $IM = \frac{1}{2}BD$ và $BD = CE$, nên $IM = \frac{1}{2}CE$.

4. **Gọi K là trung điểm của CE.**
* Suy ra $CK = KE = \frac{1}{2}CE$.
* Vậy $IM = CK = KE$.

5. **Xét tứ giác CIMK:**
* $IM // CK$ (vì $IM // AB$ và $C, A, E$ thẳng hàng).
* $IM = CK$ (chứng minh trên).
* Suy ra CIMK là hình bình hành.
* Do đó, $CM // IK$.

6. **Chứng minh I, K, B, C cùng thuộc một đường tròn:**
* Tam giác ABC cân tại A, nên $\angle ABC = \angle ACB$.
* $I$ là trung điểm của BE, suy ra $BI = IE$.
* $K$ là trung điểm của CE, suy ra $CK = KE$.
* Xét $\triangle BCI$ và $\triangle ECK$:
* $BC = AC$ (do tam giác ABC cân)
* $\angle BCI = \angle ECK$
* $CI = CK$
* Suy ra $\triangle BCI = \triangle ECK$ (c.g.c)
* Do đó $\angle CBI = \angle CEK$, tức là $\angle CBI = \angle IKB$.
* Suy ra tứ giác BCKI nội tiếp.

7. **Chứng minh B, C, M thẳng hàng:**
* Vì tứ giác BCKI nội tiếp, nên $\angle CKI = \angle CBI = \angle ABC = \angle ACB$.
* Ta có $CM // IK$ (do CIMK là hình bình hành).
* Suy ra $\angle BCM = \angle CKI = \angle ACB$.
* Do đó, $\angle BCM + \angle MCA = \angle ACB + \angle MCA = \angle ACE = 180^\circ$.
* Vậy B, C, M thẳng hàng.