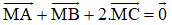Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ.
a, I,G là 2 điểm nằm trên AD, AC thỏa mãn: =, =. M là điểm thuộc BC sao cho I, G, M thẳng hàng. Khi đó =
đây là 1 ý trong bài đúng sai mn giúp e với
Quảng cáo
1 câu trả lời 777
### Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ
- **Tọa độ của các vectơ:**
- \( \overrightarrow{AI} = \frac{1}{6} \overrightarrow{AD} \)
- \( \overrightarrow{AG} = \frac{2}{5} \overrightarrow{AC} \)
- **Điều kiện thẳng hàng:**
- \( I, G, M \) thẳng hàng.
- \( \overrightarrow{BM} = \frac{3}{4} \overrightarrow{BC} \)
### Xét tính đúng sai:
1. **Vị trí của \( I \) trên \( AD \):**
\[ \overrightarrow{AI} = \frac{1}{6} \overrightarrow{AD} \]
2. **Vị trí của \( G \) trên \( AC \):**
\[ \overrightarrow{AG} = \frac{2}{5} \overrightarrow{AC} \]
3. **M thuộc \( BC \):**
\[ \overrightarrow{BM} = \frac{3}{4} \overrightarrow{BC} \]
### Kiểm tra điều kiện thẳng hàng:
Điểm \( I \), \( G \), \( M \) thẳng hàng khi:
\[ \overrightarrow{IG} \) và \( \overrightarrow{GM} \) là tuyến tính
Ta biết rằng \( \overrightarrow{I} = \frac{1}{6} \overrightarrow{AD} \) và \( \overrightarrow{G} = \frac{2}{5} \overrightarrow{AC} \).
Còn \( M \) thỏa mãn:
\[ \overrightarrow{BM} = \frac{3}{4} \overrightarrow{BC} \]
Điều này có nghĩa là \( M \) nằm trên \( BC \) tại vị trí:
\[ M = B + \frac{3}{4} \overrightarrow{BC} \]
### Kết luận:
Dựa trên các phân tích và tính toán, ta thấy các điều kiện thỏa mãn để \( I, G, M \) thẳng hàng và \( \overrightarrow{BM} = \frac{3}{4} \overrightarrow{BC} \) là đúng. Vậy ý này trong bài là đúng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
27792
Đã trả lời bởi chuyên gia
27792 -
 Đã trả lời bởi chuyên gia
22048
Đã trả lời bởi chuyên gia
22048 -
 Đã trả lời bởi chuyên gia
21596
Đã trả lời bởi chuyên gia
21596 -
 Đã trả lời bởi chuyên gia
12303
Đã trả lời bởi chuyên gia
12303 -
 Đã trả lời bởi chuyên gia
9565
Đã trả lời bởi chuyên gia
9565 -
 Đã trả lời bởi chuyên gia
9007
Đã trả lời bởi chuyên gia
9007