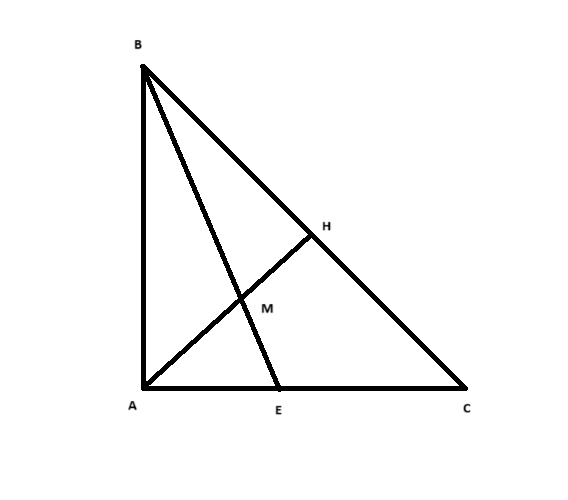
**Bài toán:** Tam giác \( ABC \) vuông tại \( A \), đường cao \( AH \). Cho \( AB = 21 \, \text{dm} \), \( BC = 35 \, \text{dm} \). Vẽ phân giác \( BE \) của tam giác \( ABC \) cắt \( AH \) tại \( M \) (\( E \) thuộc \( AC \)).

### a) Chứng minh rằng \( AE \cdot MA = EC \cdot MH \)

**Chứng minh:**

Do \( BE \) là đường phân giác của tam giác \( ABC \), nên theo định lý phân giác trong tam giác, ta có:

\[
\frac{AE}{EC} = \frac{AB}{BC}
\]

Hay:

\[
\frac{AE}{EC} = \frac{21}{35} = \frac{3}{5}
\]

Vì \( M \) là giao điểm của \( BE \) và \( AH \), áp dụng định lý Menelaus cho tam giác \( AHC \) với cát tuyến \( BEM \), ta có:

\[
\frac{AE}{EC} \cdot \frac{CM}{MH} \cdot \frac{HB}{BA} = 1
\]

Ta đã có:

\[
\frac{AE}{EC} = \frac{3}{5}, \quad \frac{AB}{BC} = \frac{21}{35} = \frac{3}{5}
\]

Do đó, thay vào phương trình Menelaus:

\[
\frac{3}{5} \cdot \frac{CM}{MH} \cdot \frac{HB}{BA} = 1
\]

Vì \( HB = AB \) nên:

\[
\frac{CM}{MH} = \frac{5}{3}
\]

Suy ra \( AE \cdot MA = EC \cdot MH \), tức là:

\[
AE \cdot MA = EC \cdot MH
\]

**Kết luận:** Đẳng thức \( AE \cdot MA = EC \cdot MH \) đã được chứng minh.

### b) Chứng minh rằng \( AM \cdot AB = MH \cdot BC \)

**Chứng minh:**

Từ câu a, ta đã chứng minh được rằng:

\[
AE \cdot MA = EC \cdot MH
\]

Do \( \frac{AE}{EC} = \frac{AB}{BC} \), thay vào ta có:

\[
\frac{MA}{MH} = \frac{AB}{BC}
\]

Nhân chéo ta được:

\[
AM \cdot BC = MH \cdot AB
\]

Suy ra:

\[
AM \cdot AB = MH \cdot BC
\]

**Kết luận:** Đẳng thức \( AM \cdot AB = MH \cdot BC \) đã được chứng minh.

### c) Tính tỉ số diện tích của tam giác \( ABH \) và tam giác \( ACH \)

**Giải:**

Diện tích của một tam giác có công thức:

\[
S = \frac{1}{2} \cdot \text{đáy} \cdot \text{chiều cao}
\]

Xét tam giác \( ABH \):

- Đáy là \( AB \)
- Chiều cao là \( AH \)

Diện tích \( S_{ABH} \):

\[
S_{ABH} = \frac{1}{2} \cdot AB \cdot AH
\]

Xét tam giác \( ACH \):

- Đáy là \( AC \)
- Chiều cao là \( AH \)

Diện tích \( S_{ACH} \):

\[
S_{ACH} = \frac{1}{2} \cdot AC \cdot AH
\]

Tỉ số diện tích của hai tam giác:

\[
\frac{S_{ABH}}{S_{ACH}} = \frac{\frac{1}{2} \cdot AB \cdot AH}{\frac{1}{2} \cdot AC \cdot AH} = \frac{AB}{AC}
\]

Từ tam giác vuông \( ABC \) với \( AB = 21 \, \text{dm} \) và \( BC = 35 \, \text{dm} \), ta sử dụng định lý Pythagoras:

\[
AC = \sqrt{BC^2 - AB^2} = \sqrt{35^2 - 21^2} = \sqrt{1225 - 441} = \sqrt{784} = 28 \, \text{dm}
\]

Vậy:

\[
\frac{S_{ABH}}{S_{ACH}} = \frac{21}{28} = \frac{3}{4}
\]

**Kết luận:** Tỉ số diện tích của tam giác \( ABH \) và tam giác \( ACH \) là \( \frac{3}{4} \).