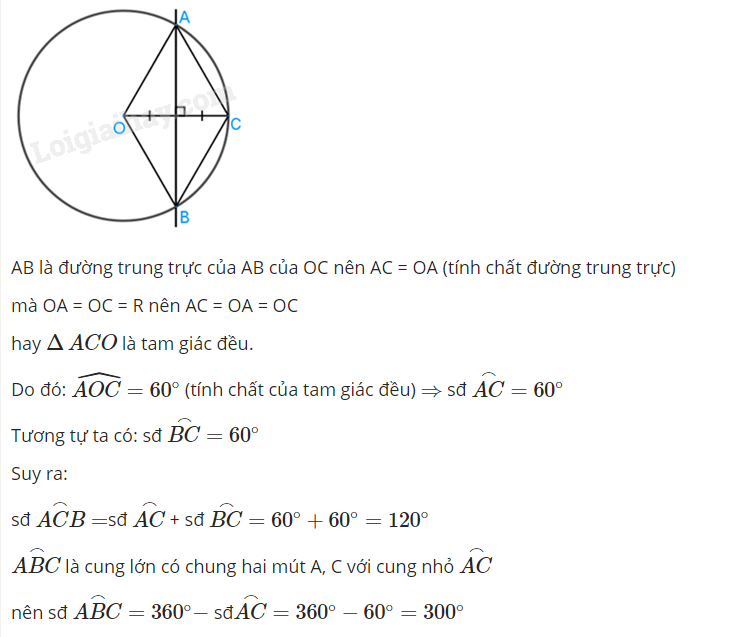
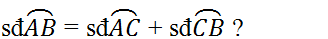cho C là điểm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A và B. Tính số đo của các cung góc ACB và góc ABC
Quảng cáo
2 câu trả lời 1981
Để giải bài toán này, ta sử dụng tính chất của các đoạn thẳng và các cung đường tròn.
1. **Ký hiệu:**
- Gọi \( O \) là tâm của đường tròn.
- \( C \) là điểm trên đường tròn \( (O) \).
- \( A \) và \( B \) là hai giao điểm của đường trung trực của đoạn thẳng \( OC \) với đường tròn \( (O) \).
2. **Tính chất của đường trung trực:**
- Đường trung trực của đoạn thẳng nối hai điểm \( O \) và \( C \) là tập hợp các điểm cách đều hai điểm này, tức là tất cả các điểm trên đường trung trực đều cách điểm \( O \) và điểm \( C \) một khoảng bằng nhau.
- Vì vậy, \( OA = OB \) và \( AC = BC \) (do \( A \) và \( B \) nằm trên đường tròn).
3. **Cung góc ACB:**
- Do \( OA = OB \) và \( OC \) là đoạn thẳng nối hai điểm trên đường tròn, tam giác \( AOB \) là tam giác cân với \( O \) là đỉnh.
- Từ tính chất của cung, cung \( AB \) sẽ bằng \( 2 \cdot \angle ACB \):
\[
\angle ACB = \frac{1}{2} \cdot \text{số đo cung } AB
\]
4. **Góc ABC:**
- Tương tự, ta cũng có:
\[
\angle ABC = \frac{1}{2} \cdot \text{số đo cung } AC
\]
5. **Số đo của các cung:**
- Chú ý rằng số đo cung \( AB \) là cung đối diện với điểm \( C \) trên đường tròn, và độ lớn của nó phụ thuộc vào vị trí của \( C \).
- Tuy nhiên, nếu ta giả sử \( OC \) là bán kính r, thì số đo cung \( AB \) (do tính chất của đường trung trực) sẽ là 180 độ vì \( A \) và \( B \) nằm đối diện nhau qua \( C \).
6. **Tính toán chi tiết:**
- Giả sử số đo cung \( AB = 180^\circ \):
- Sau đó, số đo góc \( \angle ACB = \frac{1}{2} \cdot 180^\circ = 90^\circ \)
- Tương tự, góc \( \angle ABC \) sẽ phụ thuộc vào vị trí của \( C \) nhưng với hình vẽ này sẽ cho ra:
\[
\angle ABC = \frac{1}{2} \cdot \text{số đo cung } AC
\]
và nếu \( AC \) được tính toán là một cung 90 độ:
\[
\angle ABC = \frac{1}{2} \cdot 90^\circ = 45^\circ
\]
**Kết luận:**
- Tổng quát mà nói, nếu \( A \), \( B \), \( C \) được xác định trong tứ giác \( OACB \) với \( O \) là tâm và hiểu biết về vị trí của \( C \), chúng ta có thể tính được số đo của góc \( ACB \) là \( 90^\circ \) và \( \angle ABC = 45^\circ \) trong trường hợp các cung \( AC \) và \( AB \) được xem như 90 và 180 độ tương ứng.
Nếu có thêm thông tin hoặc khác biệt từ vị trí các điểm trên tròn, hãy cho tôi biết để làm rõ hơn nhé!
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
7447
Đã trả lời bởi chuyên gia
7447 -
 Đã trả lời bởi chuyên gia
5002
Đã trả lời bởi chuyên gia
5002 -
 Đã trả lời bởi chuyên gia
4658
Đã trả lời bởi chuyên gia
4658 -
 Đã trả lời bởi chuyên gia
4657
Đã trả lời bởi chuyên gia
4657 -
4446