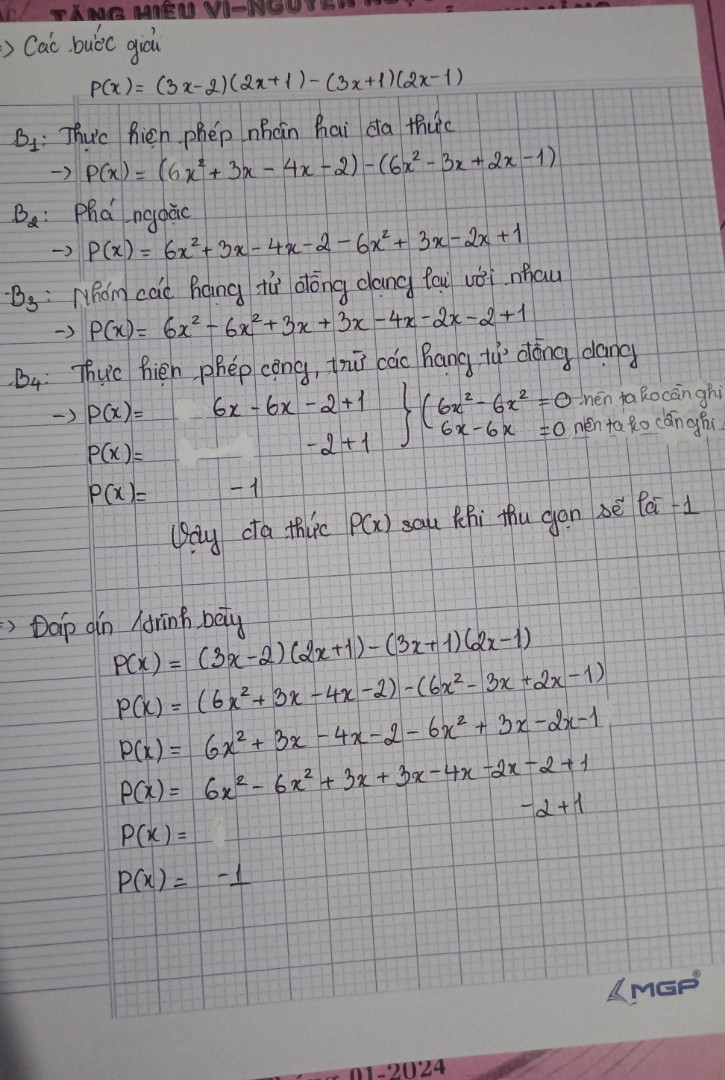Ví dụ 3: Đa thức 𝑃(𝑥) = (3𝑥 − 2)(2𝑥 + 1) − (3𝑥 + 1)(2𝑥 − 1) sau khi được thu gọn là:
Quảng cáo
3 câu trả lời 267
Để giải ví dụ này, chúng ta sẽ trước tiên thực hiện phép nhân đối với các cặp ngoặc trong biểu thức đa thức P(x):
P(x)=(3x−2)(2x+1)−(3x+1)(2x−1)
Bây giờ, thực hiện phép nhân:
1. Tính (3x−2)(2x+1):
(3x−2)(2x+1)=3x⋅2x+3x⋅1−2⋅2x−2⋅1
=6x2+3x−4x−2
=6x2−x−2
2. Tính (3x+1)(2x−1):
(3x+1)(2x−1)=3x⋅2x+3x⋅(−1)+1⋅2x−1⋅(−1)
=6x2−3x+2x−1
=6x2−x−1
Sau đó, thực hiện phép trừ (3x−2)(2x+1)−(3x+1)(2x−1):
P(x)=(6x2−x−2)−(6x2−x−1)
Khi thực hiện phép trừ này, ta loại bỏ dấu ngoặc:
P(x)=6x2−x−2−6x2+x+1
Tiếp tục rút gọn biểu thức bằng cách kết hợp các hạng tử tương đồng:
P(x)=(6x2−6x2)+(−x+x)+(−2+1)
P(x)=0+0−1
P(x)=−1
Vậy đa thức sau khi được thu gọn là:
−1
Đầu tiên, ta thực hiện phép nhân trong cặp ngoặc đầu tiên:
(3𝑥 − 2)(2𝑥 + 1) = 3𝑥 * 2𝑥 + 3𝑥 * 1 - 2 * 2𝑥 - 2 * 1
= 6𝑥² + 3𝑥 - 4𝑥 - 2
= 6𝑥² - 𝑥 - 2
Tiếp theo, ta thực hiện phép nhân trong cặp ngoặc thứ hai:
(3𝑥 + 1)(2𝑥 − 1) = 3𝑥 * 2𝑥 + 3𝑥 * (-1) + 1 * 2𝑥 - 1 * (-1)
= 6𝑥² - 3𝑥 + 2𝑥 + 1
= 6𝑥² - 𝑥 + 1
Sau đó, ta trừ kết quả của cặp ngoặc thứ hai từ kết quả của cặp ngoặc đầu tiên:
(6𝑥² - 𝑥 - 2) - (6𝑥² - 𝑥 + 1) = 6𝑥² - 𝑥 - 2 - 6𝑥² + 𝑥 - 1
= -2 - 1
= -3
Vậy sau khi được thu gọn, đa thức 𝑃(𝑥) = (3𝑥 − 2)(2𝑥 + 1) − (3𝑥 + 1)(2𝑥 − 1) là -3.
Quảng cáo
Câu hỏi hot cùng chủ đề
-
5410
-
3212
-
જ⁀➴亗ɲɦư♡
175 điểm
-
Omachi
130 điểm
-
୭୨୧Đức亗୨୧୭⚡️⚽️
110 điểm
-
sơn hoàng 30 điểm
-
Nguyễn Hồng Vương 25 điểm
-
Zin Phan 25 điểm
-
Nguyễn Thị Bảo Ngọc 20 điểm
-
Dương Thùy 20 điểm
-
Ryang Emi 20 điểm
-
sad
20 điểm
-
Bảo Nobi 20 điểm
-
Yen Vu 20 điểm
-
Thơm Nguyễn Thị 20 điểm
-
Hùng Mạnh 20 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4609
