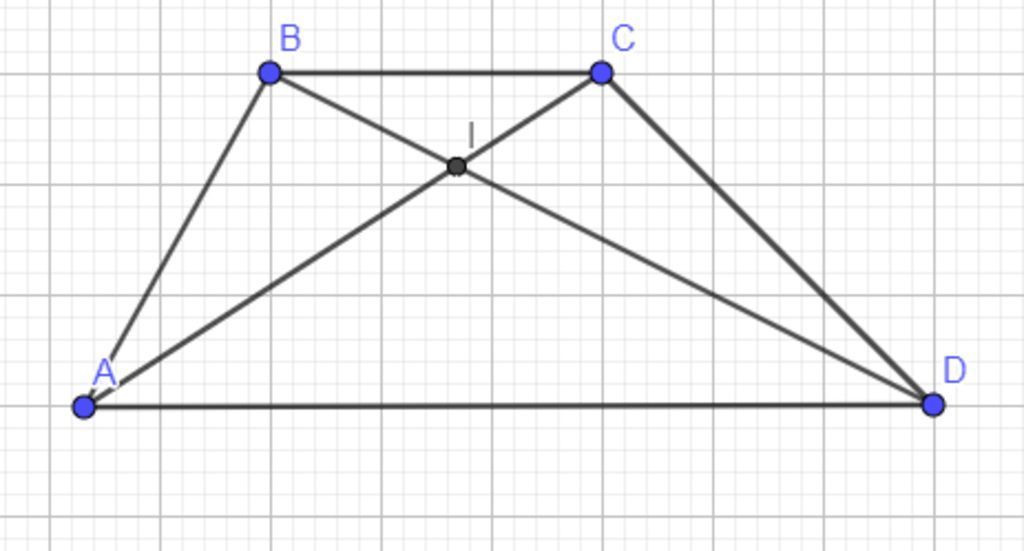
Cho hình thang ABCD có đáy Ab dài gấp ba lần đáy BC hai đường chéo AC và BD cắt nhau ở I , so sánh các diện tích tam giác sau:
a, tam giác ABC và tam giác BCD
b, tam giác BAD và tam giác CAD
c, biết diện tích tam giác ABCD bằng 48 cm². Hãy tính diện tích tam giác AIB
Quảng cáo
2 câu trả lời 207
Để giải bài toán này, chúng ta cần áp dụng các tính chất của hình thang và các tỉ lệ diện tích tam giác. Sau đây là các bước giải chi tiết:
### a. So sánh diện tích tam giác \(\Delta ABC\) và \(\Delta BCD\)
- Hình thang \(ABCD\) có \(AB \parallel CD\).
- \(\Delta ABC\) và \(\Delta BCD\) có chung đường cao kẻ từ \(C\) đến \(AB\).
Do \(AB = 3 \cdot BC\), tỉ lệ độ dài hai đáy là 3:1.
Diện tích của tam giác tỉ lệ với độ dài đáy khi có chung đường cao. Vì vậy, tỉ lệ diện tích của \(\Delta ABC\) và \(\Delta BCD\) là:
\[
\frac{S_{ABC}}{S_{BCD}} = \frac{AB}{BC} = 3
\]
Vậy, diện tích tam giác \(ABC\) gấp ba lần diện tích tam giác \(BCD\).
### b. So sánh diện tích tam giác \(\Delta BAD\) và \(\Delta CAD\)
Do hai tam giác này cùng nằm trong hình thang \(ABCD\), và hai tam giác này có chung chiều cao từ \(D\) đến \(AB\):
- \(\Delta BAD\) có đáy là \(AB\).
- \(\Delta CAD\) có đáy là \(CD\).
Tỉ lệ diện tích của \(\Delta BAD\) và \(\Delta CAD\) là:
\[
\frac{S_{BAD}}{S_{CAD}} = \frac{AB}{CD} = \frac{3CD}{CD} = 3
\]
Vậy, diện tích tam giác \(BAD\) gấp ba lần diện tích tam giác \(CAD\).
### c. Tính diện tích tam giác \(AIB\)
- Tổng diện tích hình thang \(ABCD\) là 48 cm².
- Vì tỉ lệ diện tích tam giác đã biết:
- \(S_{ABC} = 3 \cdot S_{BCD}\)
- \(S_{BAD} = 3 \cdot S_{CAD}\)
Diện tích của hình thang \(ABCD\) bằng tổng diện tích của \(\Delta ABD\) và \(\Delta BCD\):
\[
S_{ABCD} = S_{ABD} + S_{BCD} = 48 \text{ cm}^2
\]
Chia diện tích hình thang thành các tam giác nhỏ:
\[
S_{ABD} = S_{BAD} + S_{AID}
\]
\[
S_{ACD} = S_{CAD} + S_{CID}
\]
Vì hai đường chéo của hình thang chia thành 4 tam giác có diện tích tỉ lệ:
\[
\frac{S_{AIB}}{S_{CID}} = \frac{AB}{CD} = 3
\]
Đặt \(S_{CID} = x\), diện tích các tam giác còn lại là:
\[
S_{AIB} = 3x
\]
\[
S_{BAD} = 3x
\]
\[
S_{CAD} = x
\]
Tổng diện tích \(ABCD\):
\[
S_{ABCD} = S_{AIB} + S_{CID} + S_{BAD} + S_{CAD} = 3x + x + 3x + x = 8x
\]
Vậy:
\[
8x = 48 \text{ cm}^2
\]
Giải phương trình:
\[
x = 6 \text{ cm}^2
\]
Diện tích \(\Delta AIB\):
\[
S_{AIB} = 3x = 3 \times 6 = 18 \text{ cm}^2
\]
Kết luận: Diện tích của tam giác \(AIB\) là 18 cm².
Để giải bài toán này, chúng ta cần áp dụng các tính chất của hình thang và các tỉ lệ diện tích tam giác. Sau đây là các bước giải chi tiết:
### a. So sánh diện tích tam giác ΔABCΔ𝐴𝐵𝐶 và ΔBCDΔ𝐵𝐶𝐷
- Hình thang ABCD𝐴𝐵𝐶𝐷 có AB∥CD𝐴𝐵∥𝐶𝐷.
- ΔABCΔ𝐴𝐵𝐶 và ΔBCDΔ𝐵𝐶𝐷 có chung đường cao kẻ từ C𝐶 đến AB𝐴𝐵.
Do AB=3⋅BC𝐴𝐵=3⋅𝐵𝐶, tỉ lệ độ dài hai đáy là 3:1.
Diện tích của tam giác tỉ lệ với độ dài đáy khi có chung đường cao. Vì vậy, tỉ lệ diện tích của ΔABCΔ𝐴𝐵𝐶 và ΔBCDΔ𝐵𝐶𝐷 là:
SABCSBCD=ABBC=3𝑆𝐴𝐵𝐶𝑆𝐵𝐶𝐷=𝐴𝐵𝐵𝐶=3
Vậy, diện tích tam giác ABC𝐴𝐵𝐶 gấp ba lần diện tích tam giác BCD𝐵𝐶𝐷.
### b. So sánh diện tích tam giác ΔBADΔ𝐵𝐴𝐷 và ΔCADΔ𝐶𝐴𝐷
Do hai tam giác này cùng nằm trong hình thang ABCD𝐴𝐵𝐶𝐷, và hai tam giác này có chung chiều cao từ D𝐷 đến AB𝐴𝐵:
- ΔBADΔ𝐵𝐴𝐷 có đáy là AB𝐴𝐵.
- ΔCADΔ𝐶𝐴𝐷 có đáy là CD𝐶𝐷.
Tỉ lệ diện tích của ΔBADΔ𝐵𝐴𝐷 và ΔCADΔ𝐶𝐴𝐷 là:
SBADSCAD=ABCD=3CDCD=3𝑆𝐵𝐴𝐷𝑆𝐶𝐴𝐷=𝐴𝐵𝐶𝐷=3𝐶𝐷𝐶𝐷=3
Vậy, diện tích tam giác BAD𝐵𝐴𝐷 gấp ba lần diện tích tam giác CAD𝐶𝐴𝐷.
### c. Tính diện tích tam giác AIB𝐴𝐼𝐵
- Tổng diện tích hình thang ABCD𝐴𝐵𝐶𝐷 là 48 cm².
- Vì tỉ lệ diện tích tam giác đã biết:
- SABC=3⋅SBCD𝑆𝐴𝐵𝐶=3⋅𝑆𝐵𝐶𝐷
- SBAD=3⋅SCAD𝑆𝐵𝐴𝐷=3⋅𝑆𝐶𝐴𝐷
Diện tích của hình thang ABCD𝐴𝐵𝐶𝐷 bằng tổng diện tích của ΔABDΔ𝐴𝐵𝐷 và ΔBCDΔ𝐵𝐶𝐷:
SABCD=SABD+SBCD=48 cm2𝑆𝐴𝐵𝐶𝐷=𝑆𝐴𝐵𝐷+𝑆𝐵𝐶𝐷=48 cm2
Chia diện tích hình thang thành các tam giác nhỏ:
SABD=SBAD+SAID𝑆𝐴𝐵𝐷=𝑆𝐵𝐴𝐷+𝑆𝐴𝐼𝐷
SACD=SCAD+SCID𝑆𝐴𝐶𝐷=𝑆𝐶𝐴𝐷+𝑆𝐶𝐼𝐷
Vì hai đường chéo của hình thang chia thành 4 tam giác có diện tích tỉ lệ:
SAIBSCID=ABCD=3𝑆𝐴𝐼𝐵𝑆𝐶𝐼𝐷=𝐴𝐵𝐶𝐷=3
Đặt SCID=x𝑆𝐶𝐼𝐷=𝑥, diện tích các tam giác còn lại là:
SAIB=3x𝑆𝐴𝐼𝐵=3𝑥
SBAD=3x𝑆𝐵𝐴𝐷=3𝑥
SCAD=x𝑆𝐶𝐴𝐷=𝑥
Tổng diện tích ABCD𝐴𝐵𝐶𝐷:
SABCD=SAIB+SCID+SBAD+SCAD=3x+x+3x+x=8x𝑆𝐴𝐵𝐶𝐷=𝑆𝐴𝐼𝐵+𝑆𝐶𝐼𝐷+𝑆𝐵𝐴𝐷+𝑆𝐶𝐴𝐷=3𝑥+𝑥+3𝑥+𝑥=8𝑥
Vậy:
8x=48 cm28𝑥=48 cm2
Giải phương trình:
x=6 cm2𝑥=6 cm2
Diện tích ΔAIBΔ𝐴𝐼𝐵:
SAIB=3x=3×6=18 cm2𝑆𝐴𝐼𝐵=3𝑥=3×6=18 cm2
Kết luận: Diện tích của tam giác AIB𝐴𝐼𝐵 là 18 cm²
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
5117
Đã trả lời bởi chuyên gia
5117 -
 Đã trả lời bởi chuyên gia
4339
Đã trả lời bởi chuyên gia
4339